Flow over an espresso cup: Inferring 3D velocity and pressure fields from tomographic background oriented schlieren videos via physics-informed neural networks
Highlights
- Physics-Informed Neural Networks (PINN) is used to recover the velocity and pressure fields of the flow over an espresso cup by using only the temperature field provided by the Tomographic background oriented schlieren (Tomo-BOS) imaging.
- An independent Particle Image Velocimetry (PIV) experiment is conducted to validate the PINN inference for the unsteady velocity field at a center plane.
Architecture
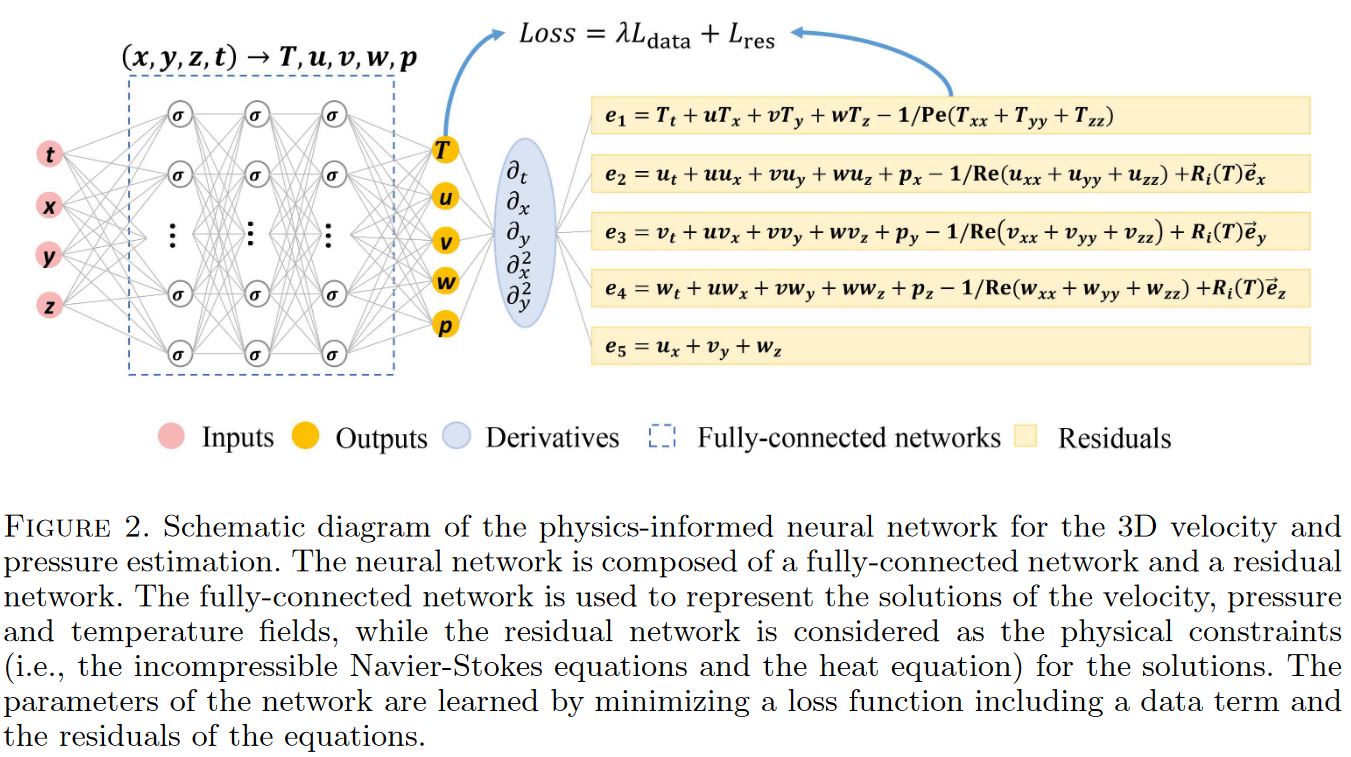
- Inputs:
- Spatio-temporal coordinates \((x, y, z, t)\)
- Outputs:
- Temperature \(T(x, y, z, t)\)
- Velocity \(u(u, v, w)\), where \((u, v, w)\) represents the velocity along \(X\), \(Y\), and \(Z\)-axis
- Pressure \(P(x, y, z, t)\)
- Loss:
- Data loss: \(L_{data}\)= Mismatch between the temperature data and the predicted temperature
- Residual loss: \(L_{res}\) = Incompressible Navier-Stokes equations and the heat equation
- Weight: \(\lambda = 100\)
- Architecture:
- 10 hidden layers, 150 neurons per layer
Benchmarking datasets
The model was trained on acquired 400 3D BOS images.
Experimental setup to acquire BOS images

Example of sequences acquired by one camera

Results
Temperature prediction

The absolute error of temperature over the whole spatial domain is less than 1℃.
Validation with the PIV experiment
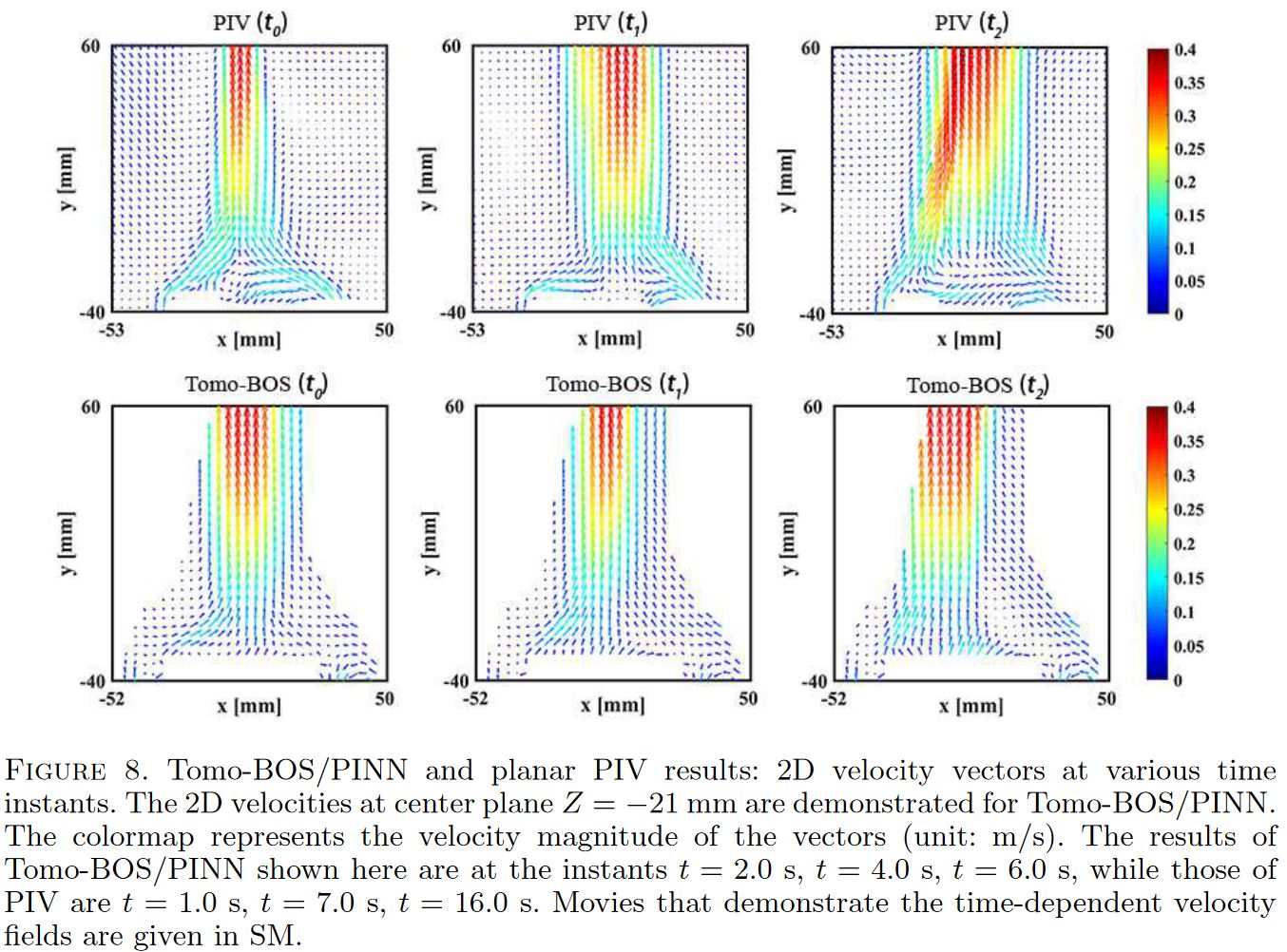 The PIV and BOS experiments were performed independently and therefore a lining up between the PIV and PINN results is not necessary.
In summary, the PIV experiment validates the PINN in terms of the velocity range.
The PIV and BOS experiments were performed independently and therefore a lining up between the PIV and PINN results is not necessary.
In summary, the PIV experiment validates the PINN in terms of the velocity range.
Training on downsampled data
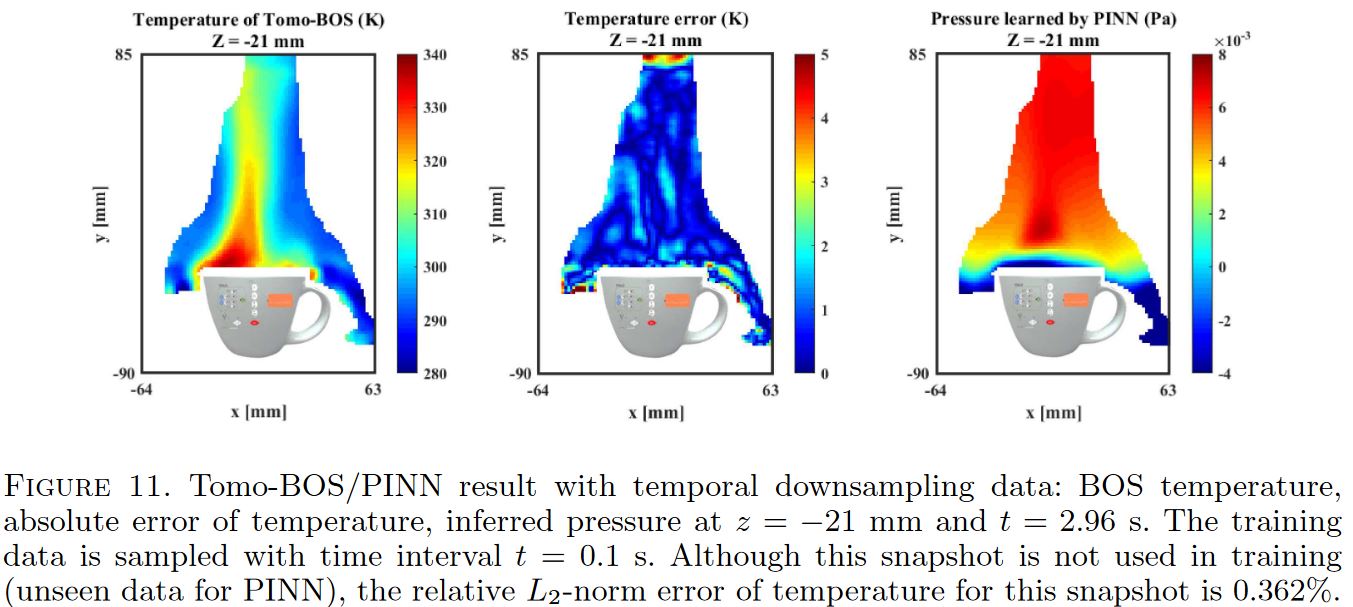
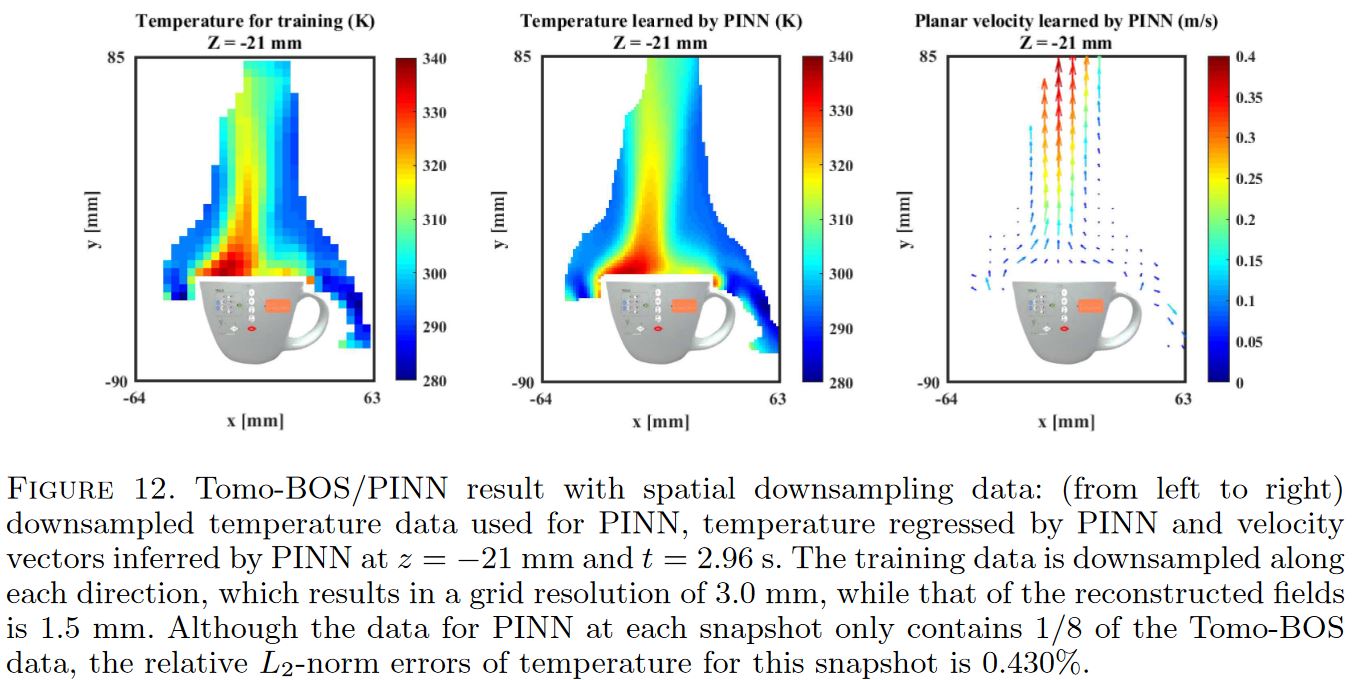 PINN performs consistently on spatial and temporal downsampling data.
PINN performs consistently on spatial and temporal downsampling data.
Conclusions
PINNs are capable of integrating the governing equations (conservation of mass, momentum, heat and mass transfer) and the temperature data, without the need to solve the governing equations using any CFD solvers. The initial conditions and boundary conditions are not required to regress the data. Moreover, PINNs can provide continuous solutions of the velocity and pressure, even if the experimental data are sparse and limited.