Notes

Inverse problem and notations

Many applications can be defined as a minimisation of two energy terms :

\[\tag{1} \operatorname*{minimize}_{x \in \mathcal{H}} f(x) + g(x)\]

with :

  • \(f\) the data fidelity term
  • \(g\) the regularization term

Let \(\Gamma(\mathcal{H})\) be the set of lower semi-continuous convex functions from a real Hilbert space \(\mathcal{H}\) to \(]-\infty, +\infty]\).

Let \(f\) and \(g\) belong to \(\Gamma(\mathcal{H})\) and \(\partial f\) and \(\partial g\) their Moreau’s subdifferential. \(x\) is a solution of (1) if :

\[\tag{2} 0 \in \partial f(x) + \partial g(x)\]

Under these assumptions, we can show that it is a special case of the following monotone inclusion problem:

\[\tag{3} \operatorname{Find} x \in \mathcal{H} \operatorname{\ such\ that\ } 0 \in \partial f(x) + A(x)\]

with \(A\) a maximally monotone operator (MMO).

To solve this problem, many methods have been introduced such as the forward backward algorithm which is expressed as :

\[\tag{4} x_{n+1} = J_{\gamma A}(x_n - \gamma \Delta f(x_n))\]

with:

  • \(J_{A} = (Id + A)^{-1}\) the resolvant of the MMO \(A\)

  • \(\gamma > 0\) a stepsize parameter

Introduction

Recently, plug-and-play approaches have been proposed to solve a regularized variational problem by replacing the operator related to the regularization term with a more sophisticated denoiser: a neural network. However, the convergence of the algorithm is originally ensured under some conditions on \(f\) and \(g\) (see above). We do not know the mathematical properties of the neural network, therefore we do not have any guarantee of the convergence of the plug-and-play approach. In this paper, the authors want to ensure its convergence by learning a neural network that mimics the mathematical properties of a maximally monotone operator (MMO).

Highlights

In this article, they propose:

  • A theorem that proves that they can approximate the resolvant of an MMO with a neural network (not detailed),
  • A framework to be able to learn the resolvant of an MMO.

Learning a maximally monotone operator

The idea is to learn the resolvant of the maximally monotone operator \(A\) : \(J_{\gamma A}\). After training, the learned resolvant can be injected in the iterative method to solve a regularized variational problem such as the forward backward algorithm :

\[\tag{5} x_{n+1} = \tilde{J}_{\theta}(x_n - \gamma \Delta f(x_n))\]

with \(\tilde{J}_{\theta}\) the learned resolvant of the MMO \(A\) with \(\theta\) parameters.

Training dataset

The aim is to learn a denoiser to afterwards plug it into the variational algorithm. Therefore they proposed to create an adapted dataset using natural images \(\bar{x}_l\) which were corrupted with Gaussian noise \(y_l\). Thus the paired images \((\bar{x}_l, y_l)\) represent respectively the groundtruth and the input data of the neural network.

Architecture of the neural network

To learn a maximally monotone operator, the neural network needs to be nonexpensive. Therefore the nonlinear activation functions need to be nonexpensive (i.e. 1-Lipschitzian). Fortunately, most of the usual activation functions are 1-Lipschitzian.

However, this is not enough to be sure that an MMO is learned. Therefore, some constraints are added during the training through the definition of the loss in order to force the learning of an MMO.

Loss

One of the properties of an MMO is the following:

A is an MMO if and only if there exists a nonexpansive (i.e. 1-Lipschitzian) operator \(Q\) such that \(J_A(x) = \frac{x + Q(x)}{2}\), that is \(A = 2(Id + Q)^{-1} -Id\)

Thus to learn an MMO, they proposed to force \(Q\) to be nonexpensive with the following constraint:

\[\left\|\nabla Q_\theta(x)\right\| \leqslant 1\]

With \(\nabla Q\) the jacobian of the operator \(Q\).

Therefore they propose to define the following loss :

\[\underset{\theta}{\operatorname{minimize}} \sum_{\ell=1}^L \left\|\tilde{J}_\theta\left(y_{\ell}\right)-\bar{x}_{\ell}\right\|^2+\lambda \max \left\{\left\|\nabla Q_\theta\left(\tilde{x}_{\ell}\right)\right\|^2, 1-\varepsilon\right\}\]

with

  • \(\lambda\) a hyperparameter to indicate the importance of the constraint on \(Q\)
  • \(\varepsilon\) a constant to ensure that \(\left\|\nabla Q_\theta(x)\right\| \leqslant 1 - \varepsilon\)

  • \( \nabla \tilde{Q}_{\theta}(x) = \nabla 2 \tilde{J}_{\theta} - Id \)

  • \(\tilde{x}_{\ell}=\varrho_{\ell} \bar{x}_{\ell}+\left(1-\varrho_{\ell}\right) \tilde{J}_\theta\left(y_{\ell}\right)\), with \(\varrho\) a random variable with uniform distribution on \([0, 1]\).

Results

Dataset used

  • Training dataset : ImageNet (50000 images)
  • Test datasets:
    • Grayscale images : BSD68
    • Color images : BSD500 and Flickr30

Neural network and variational environnement

To test their learned regularization term they focused on the following inverse deblurring imaging problems:

\[z = H \bar{x} + e\]

with:

  • \(H\) a blur operator chosen among the ones presented in Fig. 2
  • \(\bar{x}\) the original image degraded with the blur operator and a white gaussian noise
  • \(e\) a white gaussian noise
  • \(z\) the degraded image.

The purpose is to find an estimate \(\hat{x}\) from the degraded measurement \(z\).

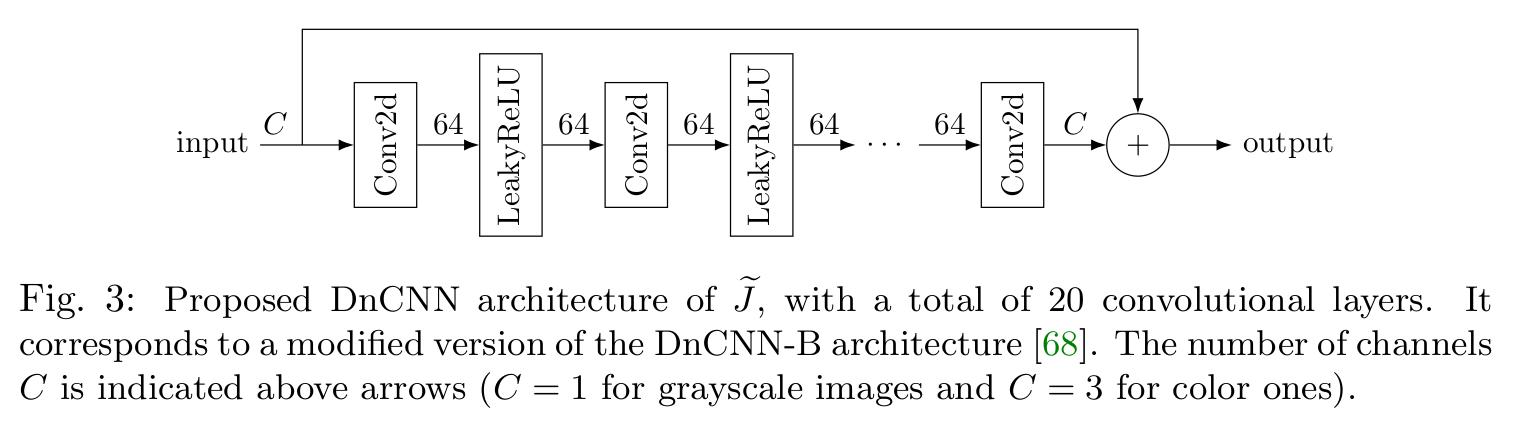
To learn the resolvant \(\tilde{J}\), they used a variant of DnCNN-B architecture that can be observed in Fig. 3.

Influence of the Jacobian penalization

They studdied the influence of \(\lambda\) on the convergence behavior of the plug-and-play algorithm by learning \(\tilde{J}\) with different \(\lambda\), fixing \(\varepsilon = 5 \times 10^{-2}\) .

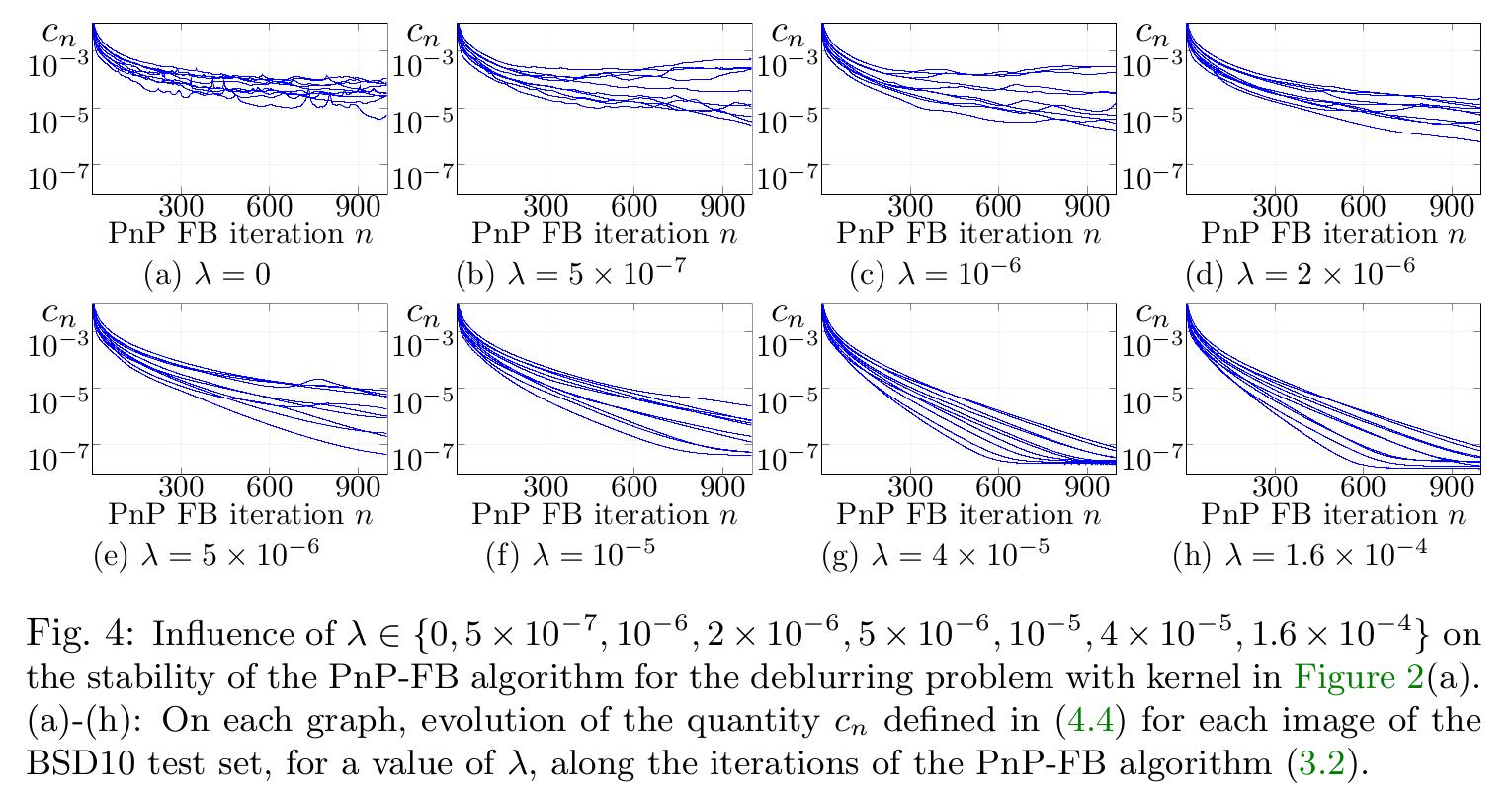
  • From \(\lambda = 10^{-5}\) the criterion \(\left\|\nabla Q_\theta(x)\right\| \leqslant 1\) is respected
  • The criterion is sufficient to observe the convergence of the algorithm
  • Metrics are maximized for \(\lambda = 10^{-5}\)

Comparison with other methods

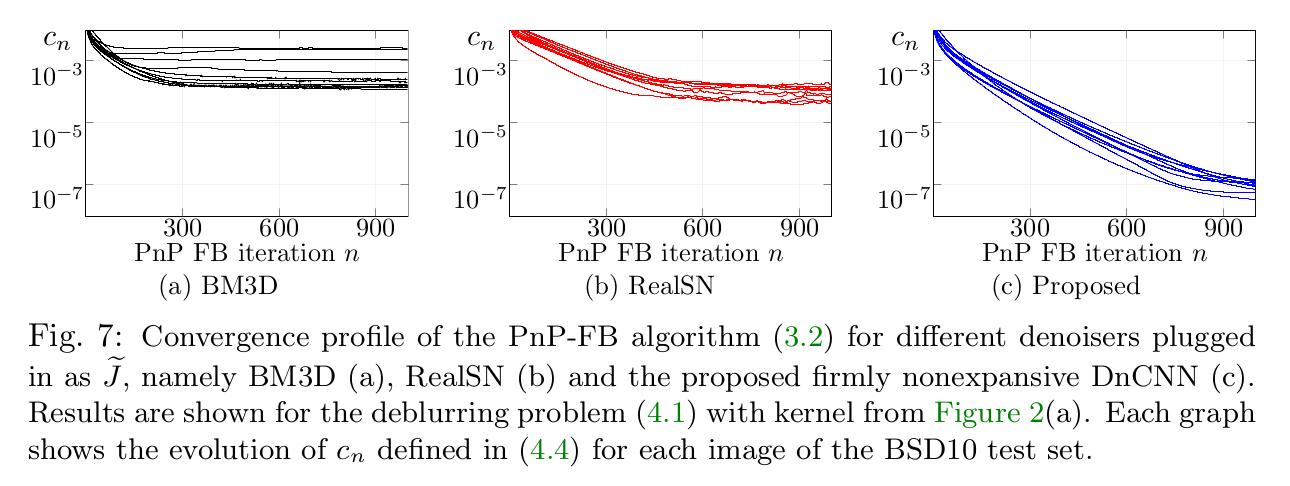
  • They analysed the convergence of the different plug-and-play algorithms. They showed that their term shows a convergence behaviour and tends to zero contrary to the other approaches, even RealSN which also aims to force the convergence of the plug-and-play algorithm.

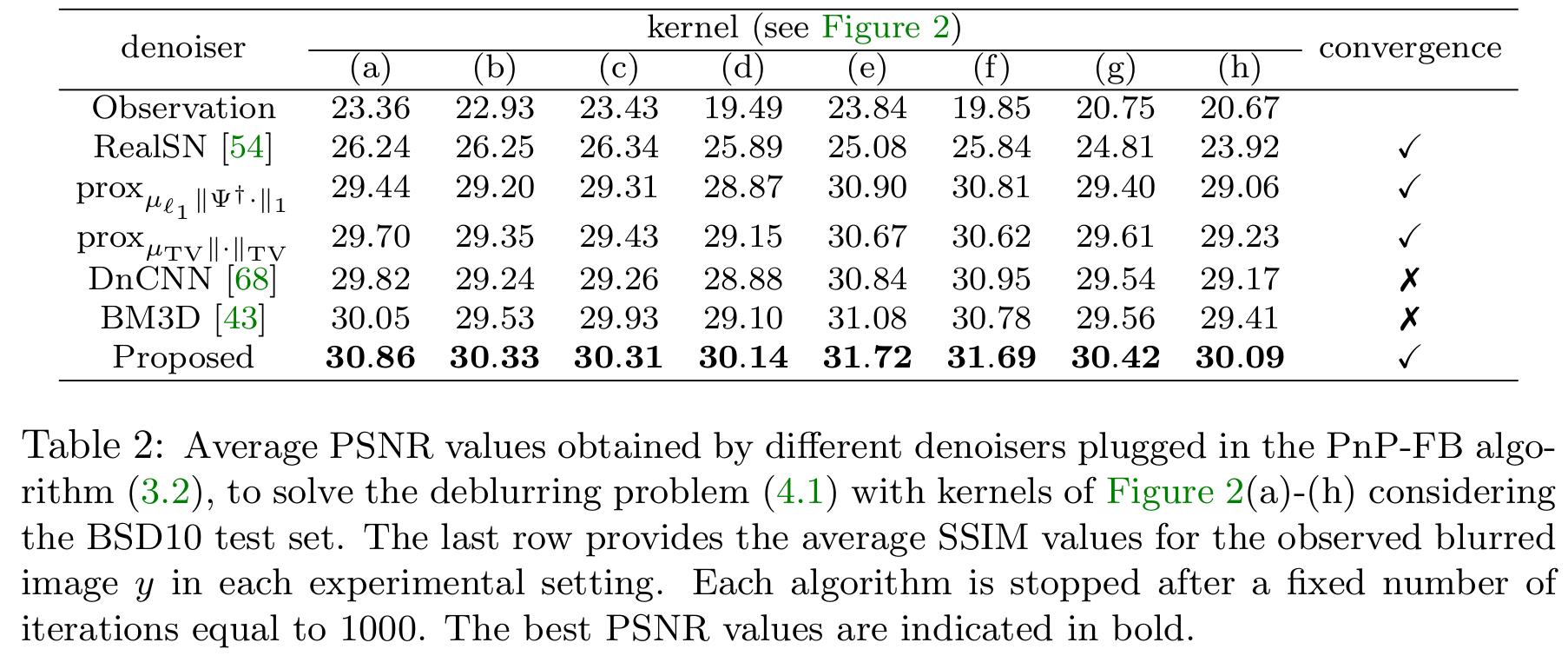
  • They showed that adding the constraint to force the convergence of the plug-and-play algorithm help to better restore the degraded images