Enhancing Pseudo Label Quality for Semi-Supervised Domain-Generalized Medical Image Segmentation
Notes
- Code is available on github
Highlights
- The goal of the paper is to obtain better quality pseudo labels when working with unlabeled images from an unknown image domain
- The contributions of the paper include a data augmentation scheme based on the Fourier Transform and a Confidence-Aware Cross Pseudo Supervision network
Introduction
Domain shifts are very common in the medical imaging field. Indeed, when working with multiple datasets, there can be a variation in the images generated due to a change of scanner, or even to a shift in the type of patient that are considered in the dataset. Therefore, when working with an already annotated dataset, acquired in a specific domain, if one wants to apply the developped networks/methods to another dataset, in another domain, it might not be trivial.
The field of domain generalization in particular tackles this issue: from a known source domain on which we can train a model, we want to obtain a generalization on a target domain for which we have no information during training.
The authors of this paper try to do this in a semi-supervised setting, where part of their training data does not have ground truth labels.
Method

Figure 1: pipeline proposed by the authors
Here, the authors take advantage of 3 source domains B, C and D, for which they have some annotations. They want to enable the generalization on a fourth domain A, for which no annotations would be available.
Data Augmentation by Fourier Transformation
Goal:
Take advantage of the low-level statistics information from the Fourier Transform images to augment the images by incorporating cross-domain info.
How?:
Two images X and X’ are randomly drawn from the source domain \(\{B,C,D\}\). The amplitudes and phase of those images are computed with the Fourier Transform: \(\mathcal{A}, \mathcal{P}, \mathcal{A}'\)
Note: The original domain of the drawn image, that is B, C or D, is unknown
The data augmentation proposed is: \(\mathcal{A}_{new}=(1-\lambda)\mathcal{A}*(1-M)+\lambda \mathcal{A}'*M\)
With:
- \(\lambda\): parameter to adjust the ratio between amplitude information from \(\mathcal{A}\) and \(\mathcal{A}'\)
- M: binary mask to adjust spatial range of amplitude spectrum to be exchanged. Set around low frequencies.
The new FT image, with magnitude \(\mathcal{A}_{new}\) and phase \(\mathcal{P}\) is transformed back into the spatial domain to give a new augmented image Z.
Confidence-Aware Cross Pseudo Supervision
There are two parallel segmentation networks \(f(\theta_{1})\) and \(f(\theta_{2})\) which have the same architecture but different intitializations.
Both X and Z go through those 2 networks, which gives four outputs \(P_F^i=f(\theta_i)(Z)\) and \(P_O^i=f(\theta_i)(X)\) for i in {1,2}.
The authors use a Cross Pseudo Supervision (CPS) scheme, developped by (Chen et al.)1: the prediction from one network is considered as a pseudo label and used to supervise the other network, and vice-versa.
In the setting introduced by the authors, with an unknown original domain for the input image (it could be B,C or D), the pseudo labels generated could have a low quality, due to the potentially high variance between samples from the different domains. Therefore, the low quality labels should have less influence: this is the Confident-Aware Cross Pseudo Supervision (CACPS) scheme introduced in the paper.
First, they take the average between the predictions from X and Z, which give the value \(P_E^1\). Then they compute the variance of predictions from X and Z as the KL-divergence: \(V_i=E[P_i^F\log(\frac{P_i^F}{P_i^O})]\). If the value is too large, it means that the labels are low quality.
They also introduce a confidence aware loss function: \(L_{cacps}=L_a+L_b\) using cross-supervision signals \(L_a = E[e^{-V_1}L_{ce}(P_E^2,Y_1)+V_1]\). \(L_{ce}\) is the cross-entropy loss and \(Y_1\) is the one-hot vector generated by the probability map \(P_E^1\).
They also use a supervision loss, based on the Dice loss: \(L_s=E[L_{Dice}(P_O^1,G)+ L_{Dice}(P_O^2,G)]\) where G is the ground truth
The training objective: \(L=L_s+\beta*L_{cacps}\)
During inference, predictions from the two networks are averaged to give the final results.
Implementation
- Segmentation networks: DeepLabv3+ with ResNet50
- Optimizer : AdamW
- Other data augmentation schemes: random rotation, scaling, crop, flip
Results
They compare themselves to supervised (nnUnet, LDDG, SAML) and semi-supervised (SDNet+Aug, Meta) methods. The metric used is the Dice.
The datasets tested are:
- Multi-centre, Multi-vendor & Multi-disease cardiac image segmentation (M&Ms) dataset (MRI, multi-label)
- Spinal Cord Gray Matter segmentation (SCGM) dataset, (MRI, mono-label)
Using n% of the dataset means:
- fully supervised setting: only n % of labeled data is used
- semi-supervised setting: training data = n% of labeled data from source domains + the rest of the dataset remains unlabeled
They test each combination of the domains A,B,C and D with 3 domains used for training.
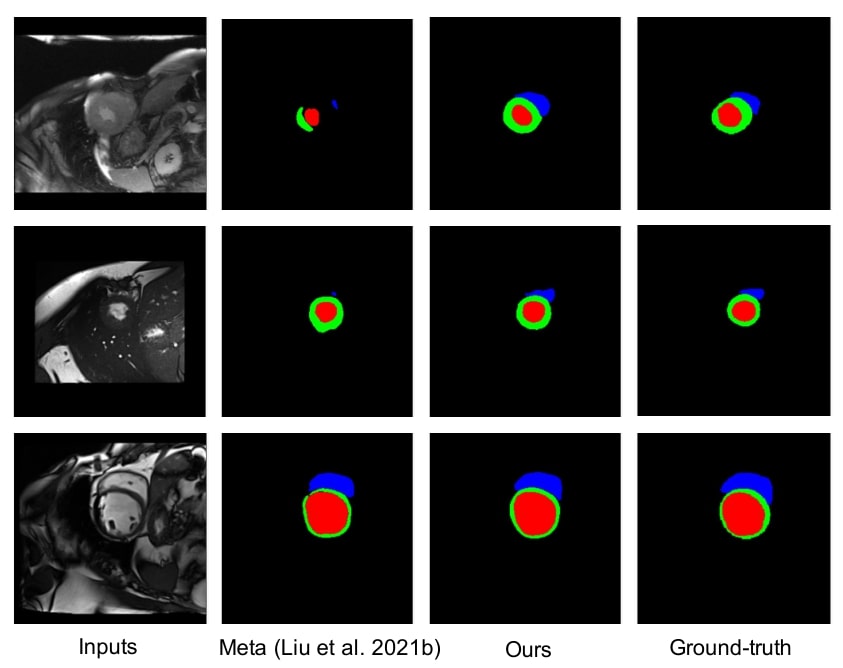
Figure 2: qualitative results on M&Ms dataset using 2% labeled data

Table 1: quantitative comparaison with SOTA method on M&Ms dataset using 2% labeled data (\(\lambda=1, \beta=3\))
The method brings better results visually and quantitatively than the baselines, even compared with Meta2, which is SOTA for semi-supervised learning and domain adaptation.
The larger improvement on domain A are explained by the fact that A is more different than the other domains.
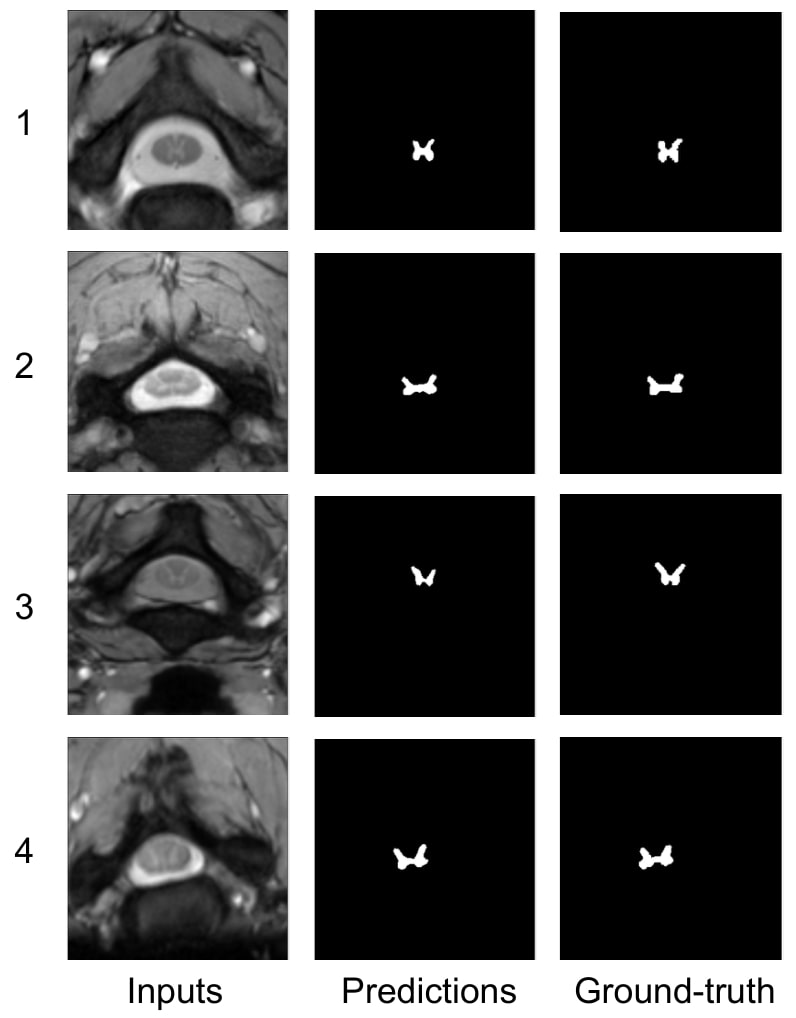
Figure 3: qualitative results on SCGM dataset using 20% labeled data

Table 2: quantitative comparaison with SOTA method on SCGM dataset using 20% labeled data (\(\lambda=0.8, \beta=1.5\))
The results are better or comparable to SOTA, in terms of metric and consistent visually with the ground truth on the four domains.
Conclusion
- Another ablation study in the same paper showed that using both Fourier DA and CACPS gives the best results.
- The two schemes introduced by this paper help getting better quality labels which means better generalization to unknown domains, without the need to have annotations of unknown domains for which generalization can be necessary.