Medical PINN: non invasive blood pressure estimation
Context
Flow around a expresso cup
- PINNs, abreviation for physics-informed neural networks, were presented by Hang Jung two years ago with his post on “Espresso Cup”.
- PINN are neural networks that embed into the loss function the knowledge of any theoretical laws, such as physical law (eg Navier-Stokes). It can be seen as a regularization term that limits the space of admissible solutions.
- In the espresso cup paper, the purpose is to perform a regression task with the estimation of pressure, temperature and velocity around a espresso cup. The loss in this paper is informed with residuals of Navier-Stockes and heat equation that we try to minimize.

- Historically, the term “PINN” was attributed to Neural Networks used for optimization and equation resolution (as a solver).
PINNs for blood pressure estimation?
- The today’s paper tackles the translation of PINNs to a medical application : the blood pressure estimation.
- We can already measure blood pressure with a cuff around the arm but it can be inconvenient for continuous measure. We would like to be able to determine blood pressure from a more convenient device such as bioimpedance electrodes:
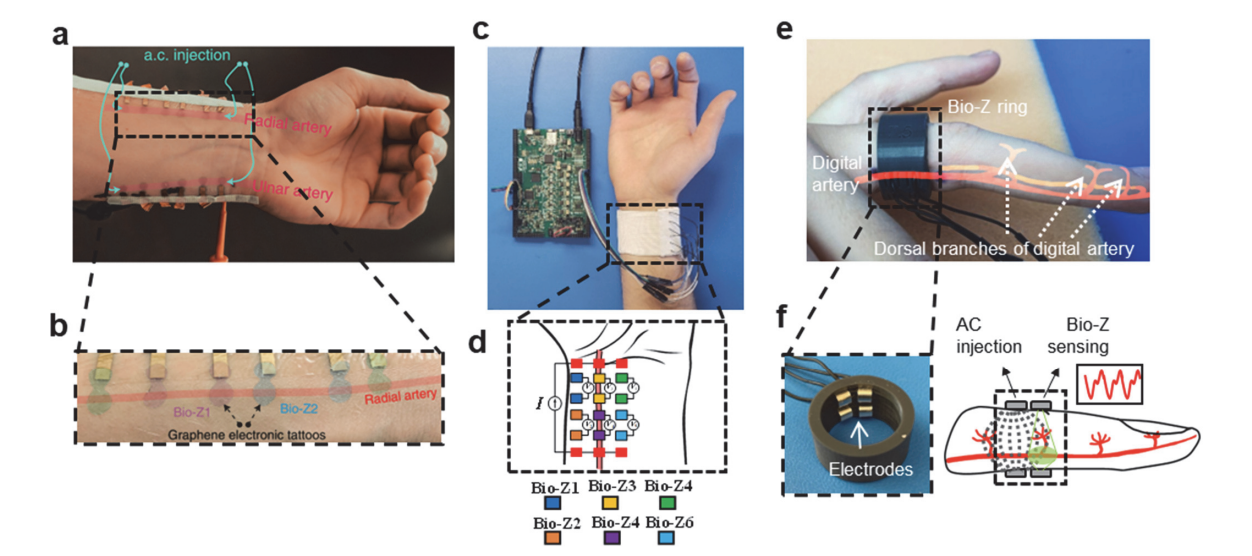
Figure 2: Bioimpedance measure with electrodes on wrist or finger
- The objective of this paper is to establish a method for blood pressure estimation with PINN using bioimpedance data and limited amount of ground truth blood pressure measures.
Methodology
Input data

Figure 3: Bioimpedance signal segmented into R cycles
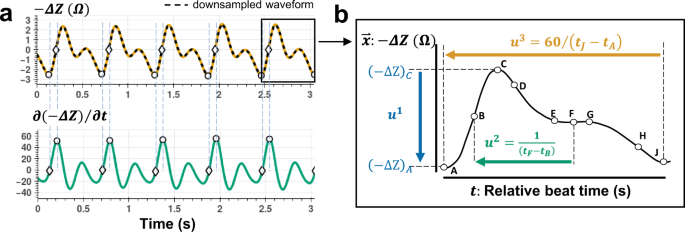
Figure 4: Feature extraction from a bioimpedance cycle: u1, u2 and u3
Outputs and ground truth
We try and estimate blood pressure characteristics such as :
- Systolic Blood Pressure (SBP)
- Diastolic Blood Pressure (DBP)
- Pulse Pressure (PP)
As a ground truth, we have blood pressure measures associated to bioimpedance cycles:
Figure 5: Association of ground truth and inputs
Architecture and Loss

Figure 6: Architecture of PINN
- Inputs:
- BioImpendance $\ BioZ$
- Bioimpedance extracted features $\ u_1$, $\ u_2$ and $\ u_3$
- Outputs:
- Blood pressure (diastolic $\ DBP$, systolic $\ SBP$,pulse pressure $\ PP$)
-
Loss \(\mathcal{L}_{supervised} = \Sigma_{i=1}^{s} (y_{i, meas}-y_{i, pred})²\) with $\ S$ being the total of ground truth measured blood pressure
\(\mathcal{L}_{physics} = \frac{1}{R-1}\Sigma_{i=1}^{R-1}\Sigma_{k=1}^{3}(y_{i+1, NN}-(y_{i, NN} + \frac{\partial y_{i, NN}}{\partial u_{i}^{k}}(u_{i+1}^{k}-u_{i}^{k})))^2\) with $\ R$ being the number of cycles for one participant inspired by the Taylor approximation : $\ y_{i+1} = y_i + \frac{\partial y_{i}}{\partial u_i}(u_{i+1}-u_{i})$
\(\mathcal{L}_{PINN} = \mathcal{L}_{supervised} + 10* \mathcal{L}_{physics}\) \(\mathcal{L}_{CNN} = \mathcal{L}_{supervised}\)
Results and conclusion
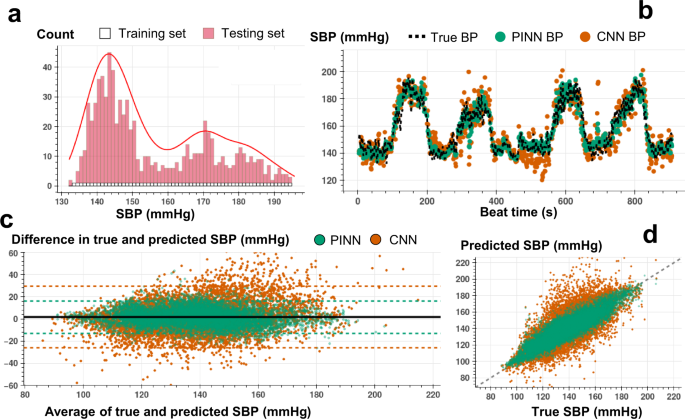
Figure 7: Comparison results of PINN vs CNN
- Prediction is continuous and more accurate .
- Feature extraction : relevant if chosen features are significant. Here $\ u_1$, $\ u_2$ and $\ u_3$ are descriptors related to cardiovascular characteristics.
- Taylor approximation : provides representation of input/ouput relation.
- Good results with minimal training data, outperforms state-of-the-art models with minimal training data.
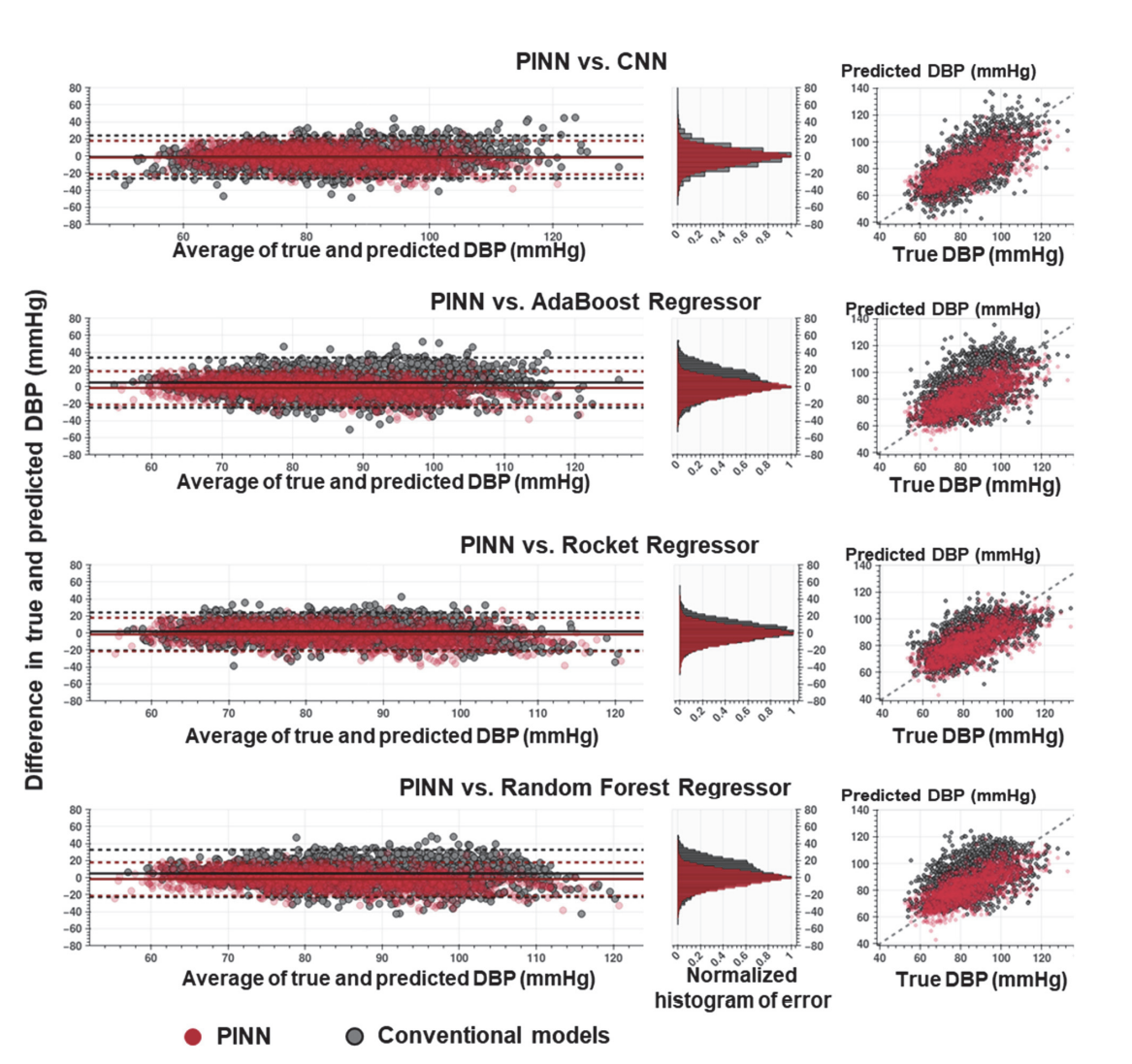
Figure 8: Comparison results PINN vs other SOTA regressor
Discussion
- The aspect “physics-informed” is in the Taylor Approximation and in the feature extraction, which both required some prior knowledge and inform the network. That being said, we can regret the absence of a physical equation. The term “physics-informed” seems abusive whereas “Theory-Trained Neural Networks” seems more appropriate.
- An ablation study to determine the importance of the features and of the time serie BioImpedance could be a interesting additional contribution.
- The contribution is more about a Proof of Concept, the experience being conducted on a small amount of young and healthy participants (15 participants, including 1 woman).