Highlights

MMultimodal representation learning is often done by aligning the representation of the unimodal views. The underpinned hypothesis is that each modality is a different view of the same entity.
However, in many real world scenarios, the interactions between the views can be more complex, as sometimes the relevant information for a target task can be found only in one modality or, even more complex, as the fusion of complementary information in all the modalities.
The authors of this paper introduce CoMM, a Constrastive Multimodal learning strategy that allows to capture redundant, unique and synergyzing information from multimodal inputs.
The code associated with the paper is available on the official GitHub repository.

Motivation

The sensorial interaction of humans with their environment is intrinsically multimodal as we constantly gather and analyze information of various types (vision, audio, smell, etc.). Similarly, many systems that we build, such as medical devices or robots, integrate information from different sensors. However, extracting and processing information from multiple sources, such as text, audio, sensors, etc., remains a challenge.

Multimodal representation learning have been explored by deep learning approches for many years now, a cornerstone work in the field being CLIP. It takes as input images with their associated caption, project both modalities with specific encoders and tries to align both latent representation through InfoNCE loss. One strong limit of this training strategy is that it only captures redundant features, i.e. all task-relevant information that is contained in all the modalities. However, in many real-case scenarios, the information can be present only in one modality, or even more complex, can be obtained only by understanding a synergetic link between the modalities.

We define redundancy (R) as a task that can be performed using either of the modialities because they contain redundant information. Uniqueness (U) refers to an information that only one of the modalities has, while synergy (S) designates a task for which both modalities have complementary information, and are needed simultaneously to fulfill the task.

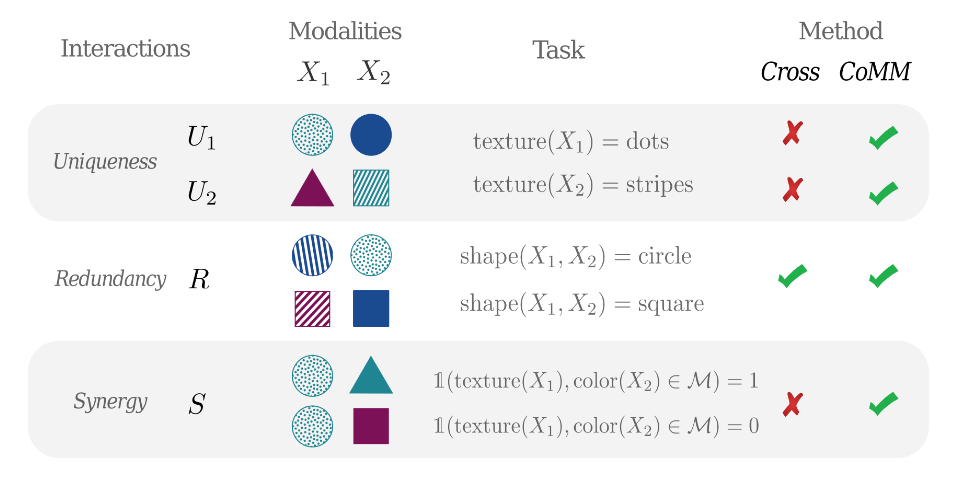
Figure 1. Illustration of the different types of interactions in a multimodal setup.

CoMM

General idea

Let \(X_1, X_2, ..., X_n\) be random variables reprensenting n different modalities and \(Y\) a given task. The goal is to learn a latent variable \(Z = f(X)\) that is a meaningful representation of \(X = (X_1,...,X_n)\) for the task \(Y\). Previous works have shown that the mutual information between the joint variable \(X=(X1,X2)\) – for simplicity, we consider a simpler case where \(n=2\) – and the task \(Y\), i.e. \(I(X;Y) = I(X_1,X_2;Y)\) can be decomposed in forms of separate interactions :

\[I(X_1,X_2;Y) = R + S + U_1 + U_2\]

where \(R\) represents the redundant, or shared, information, \(S\) the complementary information and \(U_1\) (resp. \(U_2\)) the information only present in modality 1 (resp. modality 2). There we can also decompose the following terms:

\[I(X_1;Y) = R + U_1 \\ I(X_2;Y) = R + U_2 \\ I(X_1;X_2;Y) = R - S\]

Most previous multimodal representation learning methods are limited to capturing redundant information R. A recent work introduced FactorCL which can integrate uniqueness and redundancy during the multimodal contrastive learning, but it can not capture synergy, and relies on task-specific information preserving augmentations.

Let consider a set of multimodal augmentations \(T^{*}\) such that for any \(t \in T^{*}\) and \(X' = t(X)\) we have \(I(X;X') = I(X;Y)\). Let \(f_{\theta}\) be a neural network parametrized by \(\theta\) and \(Z_{\theta} = f_{\theta}(X) = f_{\theta}(X_1,X_2)\) (resp. \(Z'_{\theta}\)) the common multimodal representation from the multimodal input \(X\) (resp. \(X'\)).

Optimizing the term \(I(Z_{\theta};Z'_{\theta})\) allows to learn the overall mutual information for the task \(Y\) \(I(X;Y) = R + S + U_1 + U_2\)
If we set \(T=\{ t_i \}\), i.e. we apply augmentations only to one modality, then optimizing \(I(Z_{\theta}; Z'_{\theta})\) allows to learn \(R + U_i\).

Model architecture and training

The architecture and training procedure proposed by the authors is quite simple, and goes as follows (Figure 2).

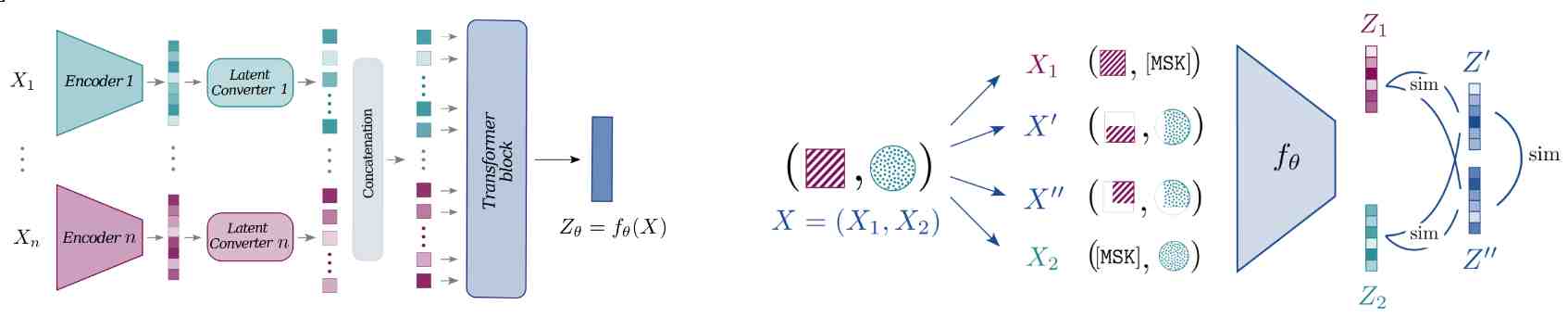
Figure 2. (left) CoMM's model architecture. Inputs from different modalities are encoded by modality-specific encoders. Modality-specific features are processed by latent converters to map them into sequences of embeddings which are concatenated and fused by a transformer block. (right) CoMM training for two modalities. Two multimodal augmentations are applied to X to obtain X' and X'', and each modality is also passed through its associated projection operator. The n+2 transformed versions of X are processed by the network and trained to maximize their agreement using contrastive objectives.

Each modality is encoded independently by its specific encoder
Linear modules transform features into modality-specific sequences of embeddings
The embeddings of all modalities are concatenated and fused by self-attention layers to obtain the final multimodal embedding \(Z\).

Given multimodal input \(X=(X_1,...,X_n)\) and a set of label-preserving multimodal transforms \(T^{*}\), two random augmentations \(t',t''\) are drawn from \(T^{*}\) and applied to \(X\) to obtain \(X' = t'(X)\) and \(X'' = t''(X)\). We also consider the projections \(X_i = ( [MASK],...,X_i,...,[MASK] )\) for \(i \in \{ 1,...n, \}\) which mask every modality except for the \(i\)-th. For one multimodal input, it gives \((n+2)\) transformed versions of the input, which we all encode by the network to obtain their corresponding embeddings : \(Z'\), \(Z''\) and \(\{ Z_i\}_{i=1}^{n}\). As briefly discussed before, several terms are optimized during the training : \(I(Z';Z'')\) to maximize \(R + S + \sum_{i} U_i\) and \(I(Z_i;Z')\) and \(I(Z_i;Z'')\) to better approximate \(R + U_i\). The authors used the InfoNCE loss to optimize their network:

\[\hat{I}_{\textrm{NCE}}(Z,Z') = \mathbb{E}_{z,z'_{pos},z'_{neg}} \left[ \log \frac{\textrm{exp sim}(z,z'_{pos})}{\sum_{z'_{neg}} \textrm{exp sim}(z,z'_{neg})} \right]\]

The overall optimization objective is the following:

\[\mathcal{L}_{\textrm{CoMM}} = - \underbrace{\hat{I}_{\textrm{NCE}}(Z',Z'')}_{\approx R + S + \sum_{i=1}^{n}U_i} - \sum_{i=1}^{n} \underbrace{\frac{1}{2} \left( \hat{I}_{\textrm{NCE}}(Z_i,Z') + \hat{I}_{\textrm{NCE}}(Z_i,Z'') \right)}_{\approx R+U_i} =: \mathcal{L} + \sum_{i=1}^{n}\mathcal{L}_i\]

Experiments

The authors conducted two main sets of experiments. First, they used a synthetic dataset to define a controlled environment and investigate the benefits of their model for capturing redundancy, uniqueness and synergy. Second, they evaluate their self-supervised learning method on various benchmarks (see Figure 3 for examples).

Synthetic bimodal trifeature dataset

The trifeature dataset contains images of one of ten shapes (round, square, star, etc.), with one of ten textures (dots, stripes, etc.) and one of ten colors, for a total of 1 000 combinations. A fake bimodal dataset is created by taking two different images from the Trifeature dataset.

Figure 3. Examples of images sampled from the Trifeature dataset.

Redundancy. To model redundancy, shape is chosen as shared feature between the modalities. It means that each time a pair is sampled and given to the bimodal neural network, the first image and the second image always have the same shape. The ability of the latent representation to capture this redundant feature is evaluated by the linear probing accuracy of shape prediction (change level of 10%). Training and test sets follow the same distribution with respectively 10 000 and 4096 images.

Uniqueness. Texture is chosen as the unique feature in the bimodal dataset. For a given pair of images (with similar shape) which form the bimodal input, the two images have different textures. The capacity of the model and the output multimodal latent representation \(Z\) to capture unique information is measured by the linear probing accuracy to predict the texture of the first image. The same metric is measure with the texture of the second image (chance level of 10%). Training and test sets follow the same distribution with respectively 10 000 and 4096 images.

Synergy. Modelling and measuring synergy is trickier. To do so, the authors have introduced bias in the training set between the two modalities. In the two previous experiments, the color and texture of the two images and drawn independently. In this experiment, they define a mapping \(\mathcal{M}\) between the ten textures and ten colors. They randomly selected 10 000 pairs of images respecting this mapping for the training. The test set is the same as above, and the task is here to predict whether an image satisfies the mapping \(\mathcal{M}\) or not (change level of 50%).

The performance on the three tasks are shown in Figure 4. While redundacy information is easily captured by all methods, uniqueness can not be seen with standard multimodal alignment. CoMM is the only method to accurately capture synergyzing information between two modalities.

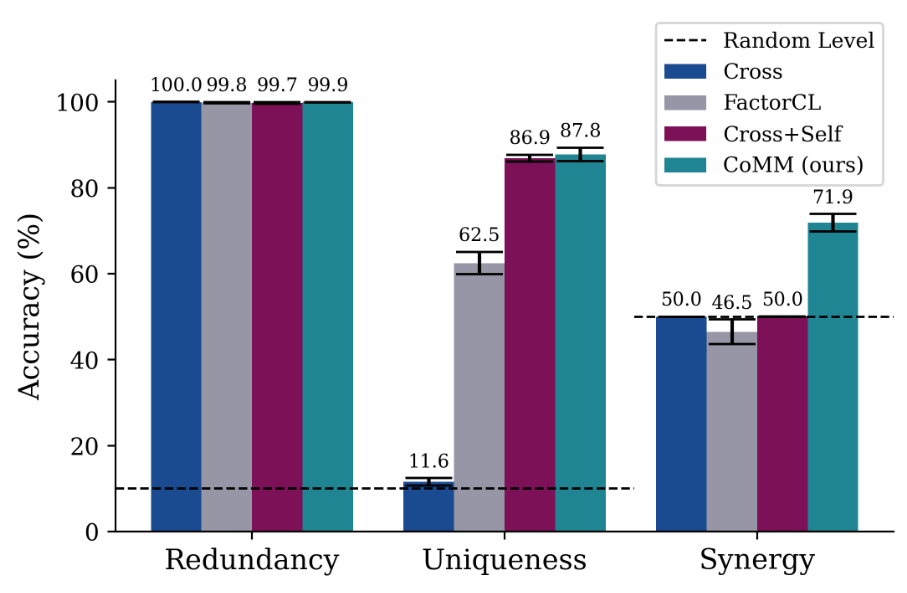
Figure 4. Linear probing accuracy of redundancy, inuquenesss and synergy on bimodal Trifeature dataset.

Real-world benchmarks

The authors assessed the effectiveness of their self-supervised method on several real-world benchmarks :

Multibench : they consider various subsets of data types and tasks in the MultiBench dataset, including Vision&Touch (robotic dataset with images, force and proprioception data), MIMIC (mortality and disease prediction from medical reconds such as tabular data and medical time series), MOSI (sentiment analysis from video), UR-FUNNY (humor detection from videos) and MUs-TARD (sarcasm detection from TV shows).
Multimodal IMBd : the task is to predict the genre(s) of a movie using its poster (image) and plot’s description (text).

For each dataset and task, they consider either a self-supervised setup, in which they pre-train the model and evaluate with linear probing, or a supervised setup, where the model is fully fine-tuned. Performance results for these datasets and tasks are given in Figure 5 and 6.

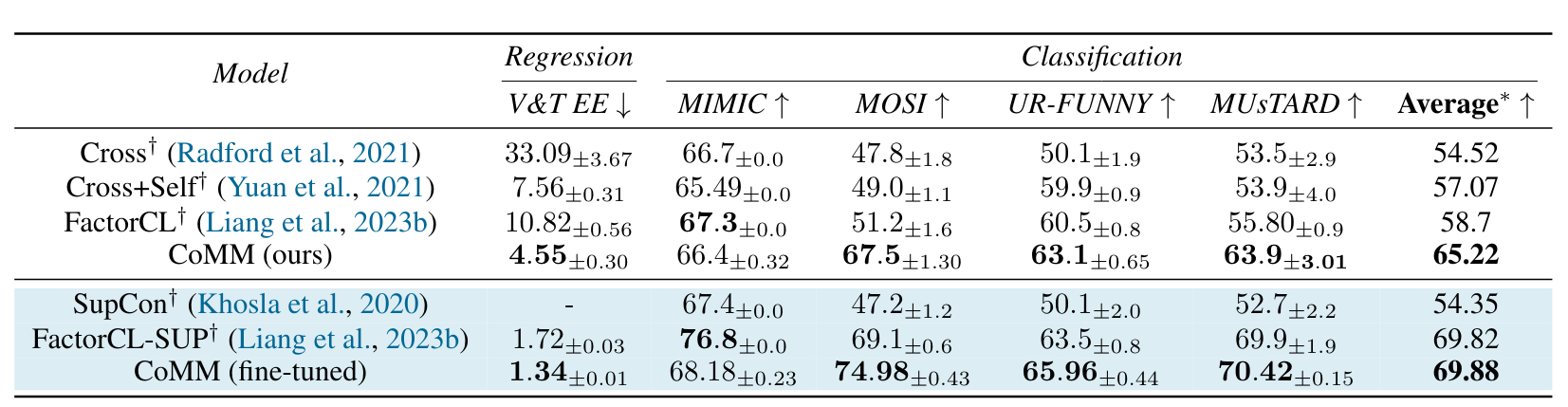
Figure 5. Performance on Multibench. Rows in blue are supervised.

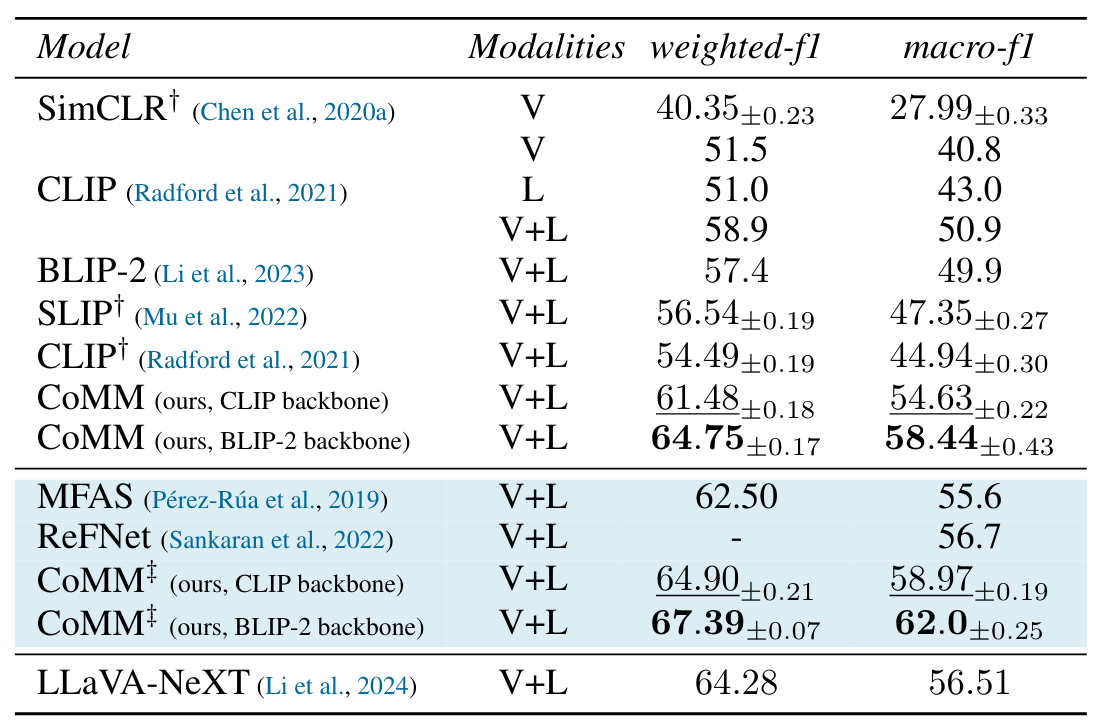
Figure 5. Performance on MM-IMBd. Rows in blue are supervised.

Ablation study

The paper includes several ablation studies to evaluate th importance of the design choices of the model on its performance (latent projections, data augmentation types, etc.). The most interesting study in my opinion is the influence of the terms in the training loss (Figure 6). Interestingly, minimizing the loss \(\mathcal{L}\) allows to learn synergy at a very slow pace. The authors argue that this is because the modal has to learn modality-specific features first (first halves of the performance curves) before learning interactions (second halves of the curves). Their loss \(\mathcal{L}_{\textrm{CoMM}}\) speeds up this learning process.

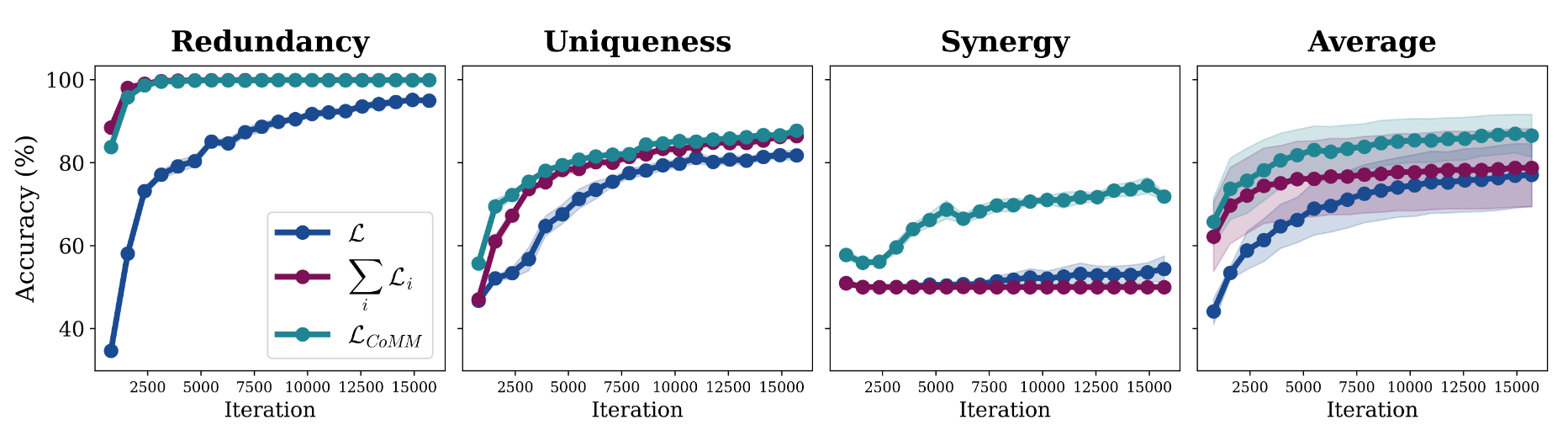
Figure 6. Linear probing accuracies on biomdal Trifeature dataset of redundancy R, uniqueness U and synergy S depending on the loss function.

Conclusion

In this paper, the authors explore multimodal self-supervised learning through the lens of three concepts: reduncancy, uniqueness and synergy. They propose a new model that solves the limitations of current models, and in particular enables better capture of complementary information between the different input modalities. Their work has a few limitations, the two main being the high computational cost for data augmentation in their training, and the lack of experiments in a setting with more than two modalities.