Notes

  • Link to the code here

Diffusion model reminders

The full presentation, including links to the diffusion model (DDPM), is available here

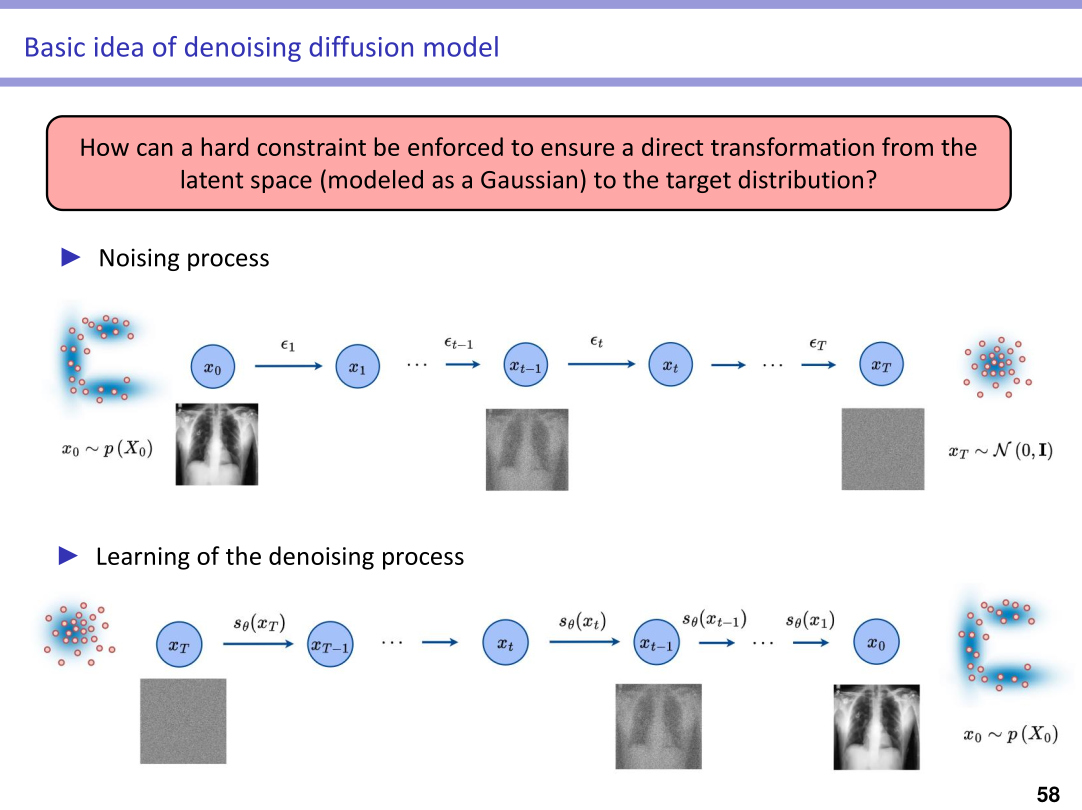
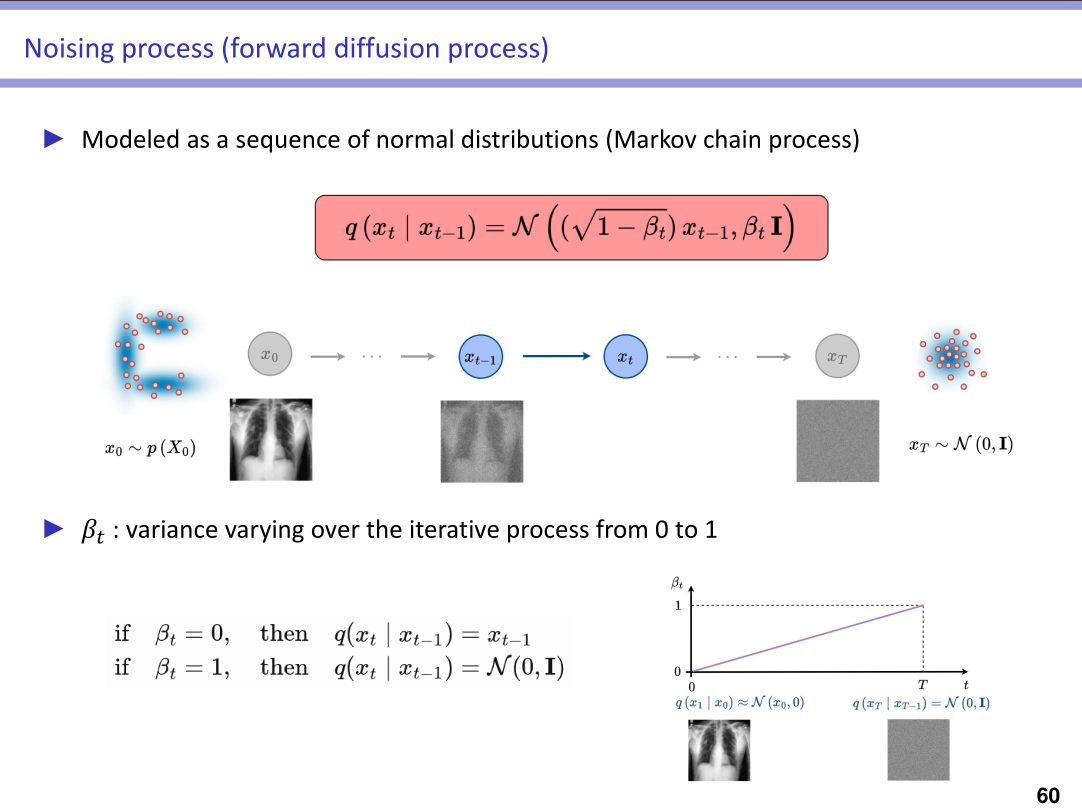
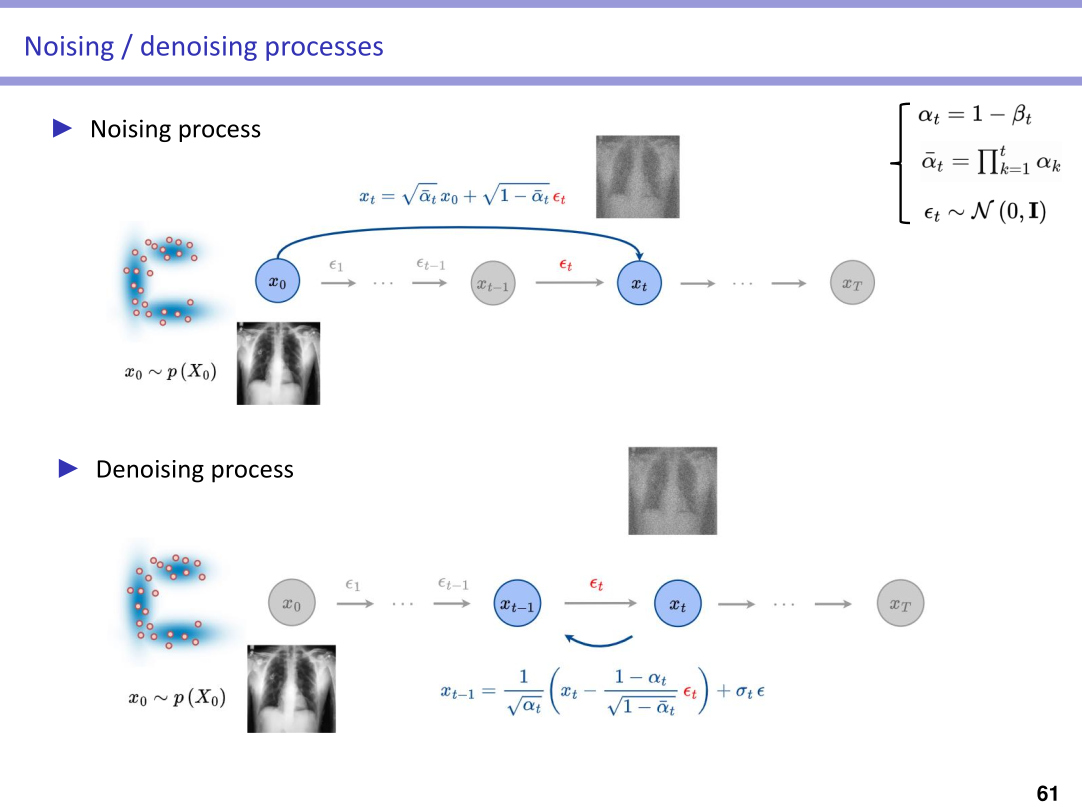
Highlights

  • Design of an implicit guidance within diffusion models to facilitate optimal image restorations and improve the accuracy of anomaly segmentation
  • Evaluation from three public datasets: IXI Dataset (brain T1-weighted MRI scans from 582 patients), ATLAS 2.0 (655 T1-weighted MRI scans accompanied by expert-segmented lesion masks + 217 healthy samples), and GRAZPEDWRI-DX dataset (10,643 X-rays of pediatric wrist injuries from 6,091 individual pa- tients)

Motivations

  • By adding and removing noise, DDPMs transform pathological inputs into pseudo-healthy outputs, demonstrating efficient generative potential
  • The intrinsic noise-dependent process can result in significant loss of information, leading restored images to deviate from their original state, including in regions unaffected by pathology

key idea

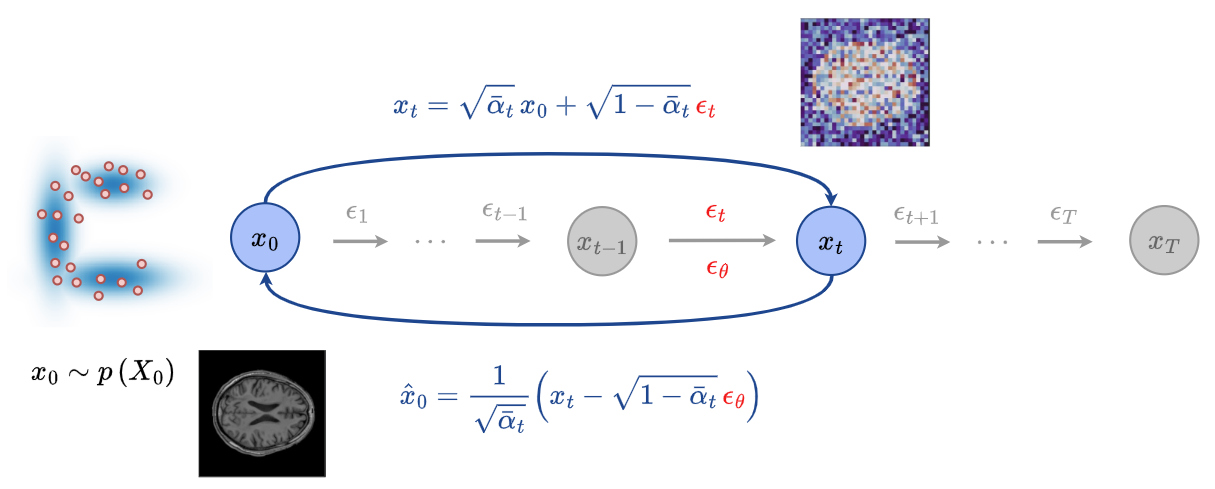
  • At any time step \(t\) of the reverse process, it is possible to reconstruct an estimate of the input image \(x_0\), denoted \(\hat{x}_0\), using the following equation
\[\color{red}{\hat{x}_0(x_t,t) = \frac{1}{\sqrt{\bar{\alpha}_t}} \left(x_t - \sqrt{1-\bar{\alpha}_t}\, \epsilon_\theta(x_t,t) \right)}\]
  • This makes it possible to supervise the reconstructed image during the reverse process and to leverage this supervision to improve the generation of the pseudo-healthy output

Methodology

Training procedure

Modeling the normal feature space

  • Excusively healthy subjects are used during training: \(\{x^{(i)}\}_{i=1}^{N}\) with \(x^{(i)} \in \mathbb{R}^{H \times W \times C}\)
  • No pre-trained Variational Autoencoder is used; the method operates directly in the image space. The images are resized to dimensions of \(128 \times 128\)

Diffusion process

  • A standard DDPM is used to learn the reconstruction of images from healthy subjects

Inference

Implicit Guidance via Intermediate Anomaly Maps

  • Intermediate anomaly maps are introduced to enable harmonization throughout the reverse process at specific time steps

  • At each pre-defined specific time-step \(t\), an estimation of the pseudo-healthy image is computed as:

\[\hat{x}^t_0 = \frac{1}{\sqrt{\bar{\alpha}_t}} \left(x_t - \sqrt{1-\bar{\alpha}_t}\, \epsilon_\theta(x_t,t) \right)\]
  • These maps compare the predictive reconstructions \(\hat{x}^t_0\) with the actual input image \(x^{\text{input}}_0\), highlighting discrepancies that indicate anomalies and distinguishing regions that are likely healthy

Anomaly maps

  • Anomaly maps \(m\) combine residual differences with the Learned Perceptual Image Patch Similarity (LPIPS) metric 1, enhancing the identification of subtle pathological changes
\[m(x,x_{rec}) = |x-x_{rec}| \cdot S_{LPIPS}(x,x_{rec})\]
  • Each mask \(m\) is normalized to the range \([0,1]\) and processed using morphological operations, consisting of a closing followed by a dilation, denoted as \(cd\)
  • These anomaly maps are subsequently used in the harmonization process to produce reconstructions that not only closely resemble the original images but also conform to healthy tissue profiles
\[\hat{x}_0 = cd\left( m(\hat{x}^t_0,x^{\text{input}}_0) \right) \cdot \hat{x}^t_0 + \left( 1 - cd\left( m(\hat{x}^t_0,x^{\text{input}}_0) \right) \right) \cdot x^{\text{input}}_0\]
  • \(\hat{x}_0\) is then used to recompute \(x_t\) following the standard diffusion process, i.e.
\[x_t = \sqrt{\bar{\alpha}_t} \, \hat{x}_0 + \sqrt{1-\bar{\alpha}_t} \, \epsilon_t\]
  • The reverse process then continues until the next harmonization step

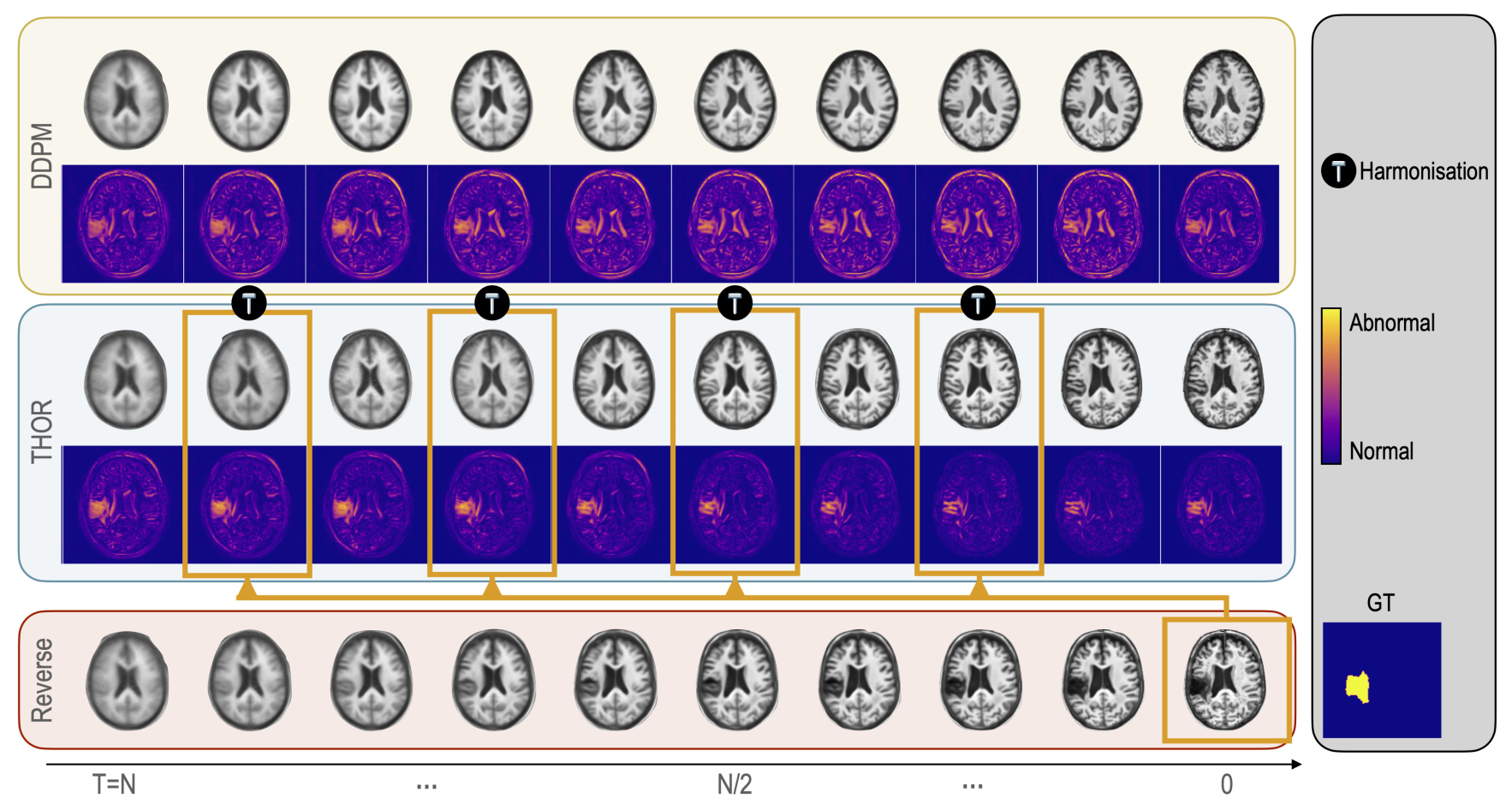
Final anomaly map

  • the final anomaly map \(S\) is computed using the harmonic mean of the anomaly maps at the selected timesteps, defined as

    \(\displaystyle S = n \, \Big/ \, {\sum_{t \in \text{selected steps}} \frac{1}{m(\hat{x}^t_0,x^{\text{input}}_0)}}\)

    where \(n\) is the total number of selected harmonization timesteps

Experiments

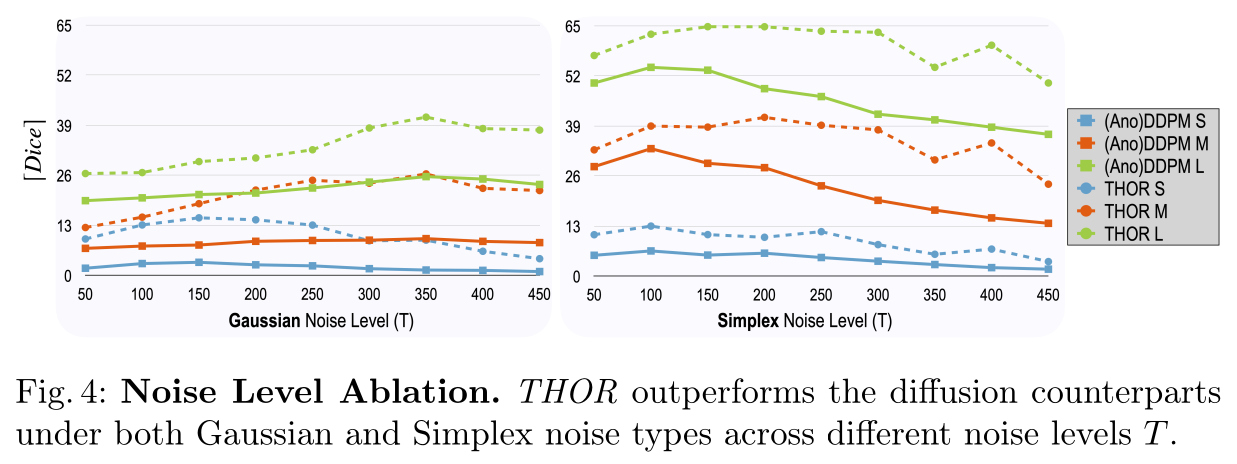
  • During inference, both Gaussian and Simplex noise are evaluated, with the noising process applied up to \(T = 350\) for Gaussian noise and up to \(T = 250\) for Simplex noise

Results

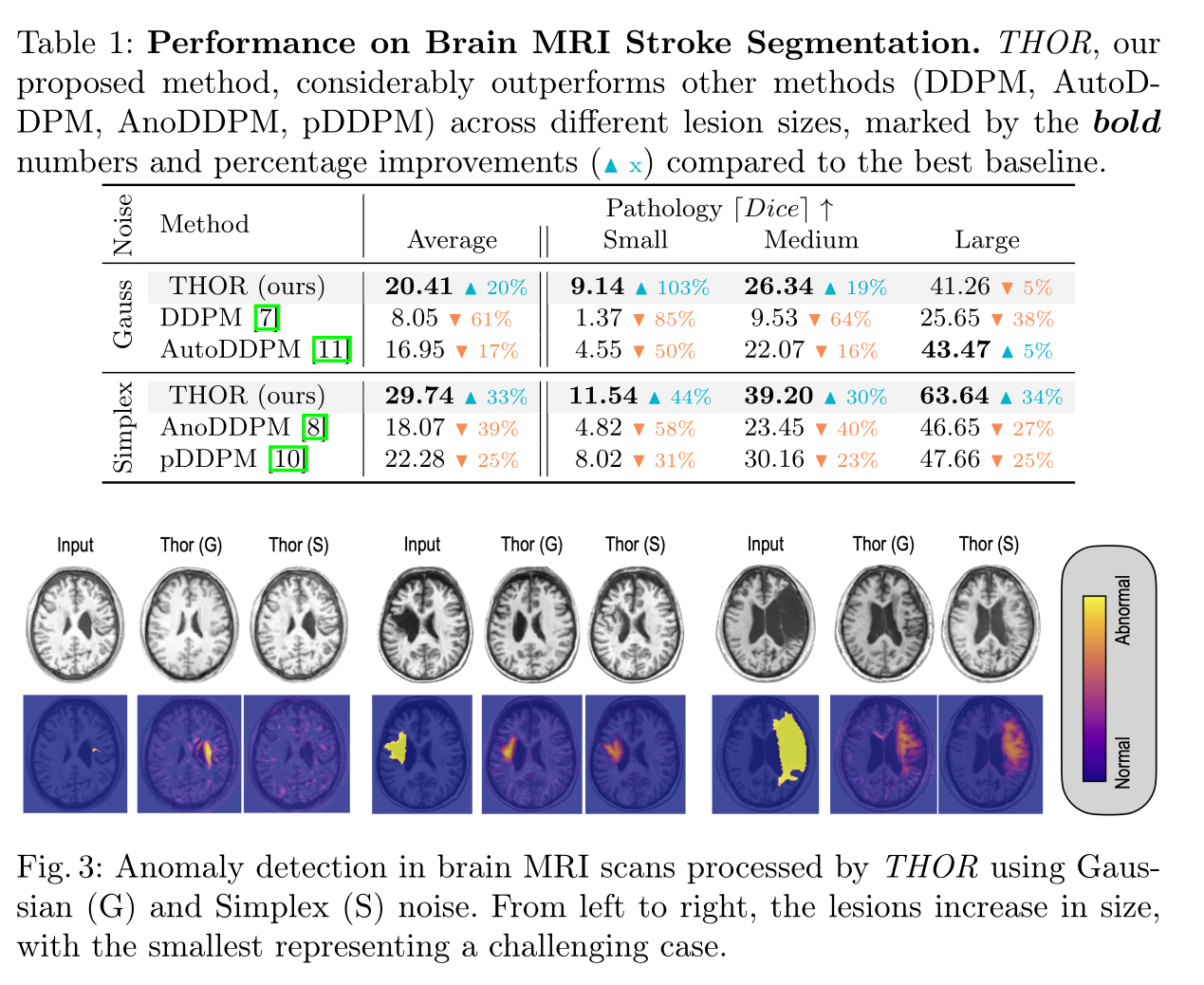
Ischemic Stroke Lesion Segmentation in Brain MRI

  • The training dataset encompasses \(582\) T1-weighted MRI scans from the IXI dataset and \(217\) healthy samples from the ATLAS v2.0 dataset
  • ATLAS dataset was used for testing, which includes \(655\) T1w MRI scans with expertly segmented lesion masks
  • Scans were normalized to the \(98\)th percentile and resized to \(128 \times 128\) pixels, with lesion segmentation evaluated via the maximum achievable Dice

 

Sensitive analysis of noise level \(T\)

 

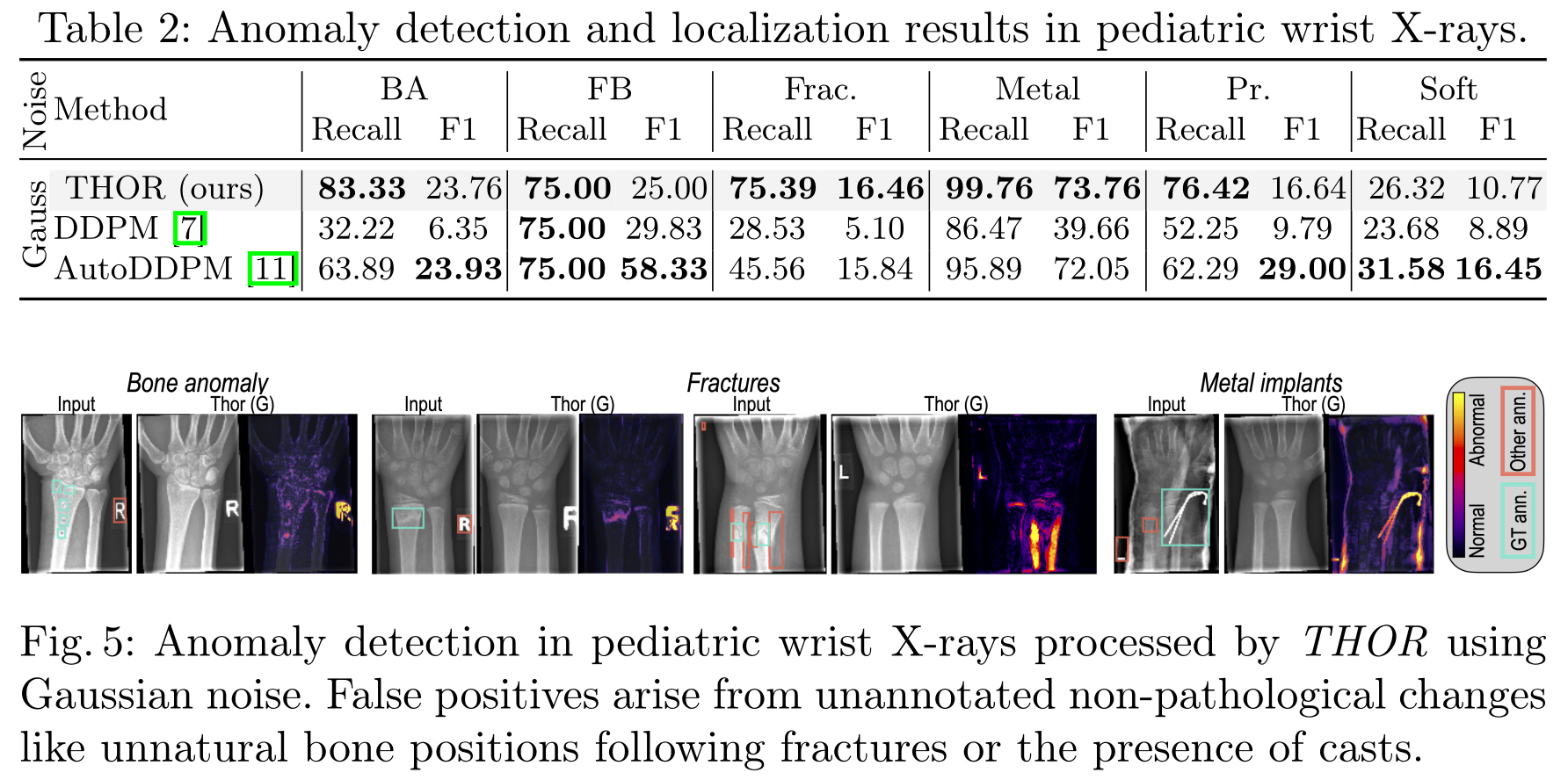
Anomaly Localization in Pediatric Wrist X-rays

  • GRAZPEDWRI-DX dataset is used, which contains 10,643 X-rays of pediatric wrist injuries from 6,091 individual patients
  • It includes a wide array of anomalies annotated with bounding boxes by certified pediatric radiologists. This includes bone anomalies (BA), foreign bodies (FB), fractures (Frac.), the presence of metal implants, periosteal reactions (PR), and soft tissue conditions (Soft).
  • Recall and F1 scores are reported

 

Conclusions

  • This paper presents an unsupervised anomaly detection
  • The proposed method incorporates a novel harmonization process to enhance the denoising and restoration, thereby improving segmentation accuracy
  • The method beats state-of-the-art methods on two different settings involving three different datasets

Reference

  1. Zhang, R., Isola, P., Efros, A.A., Shechtman, E., Wang, O. The unreasonable effectiveness of deep features as a perceptual metric, IEEE/CVF Conference on Computer Vision and Pattern Recognition 2018 ↩