Notes

  • Link to the code here

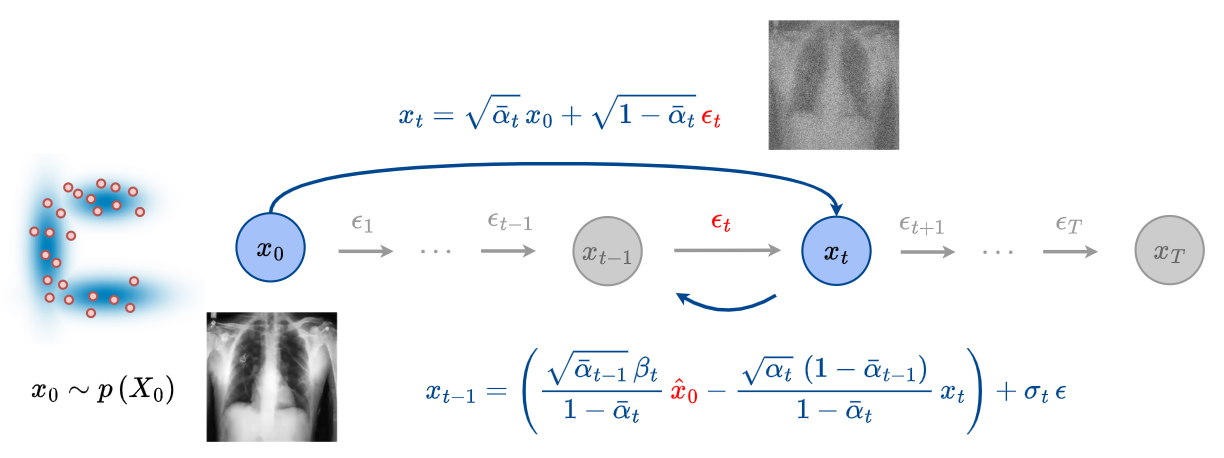
Diffusion model reminders

The full presentation, including links to the diffusion model (DDPM), is available here

 

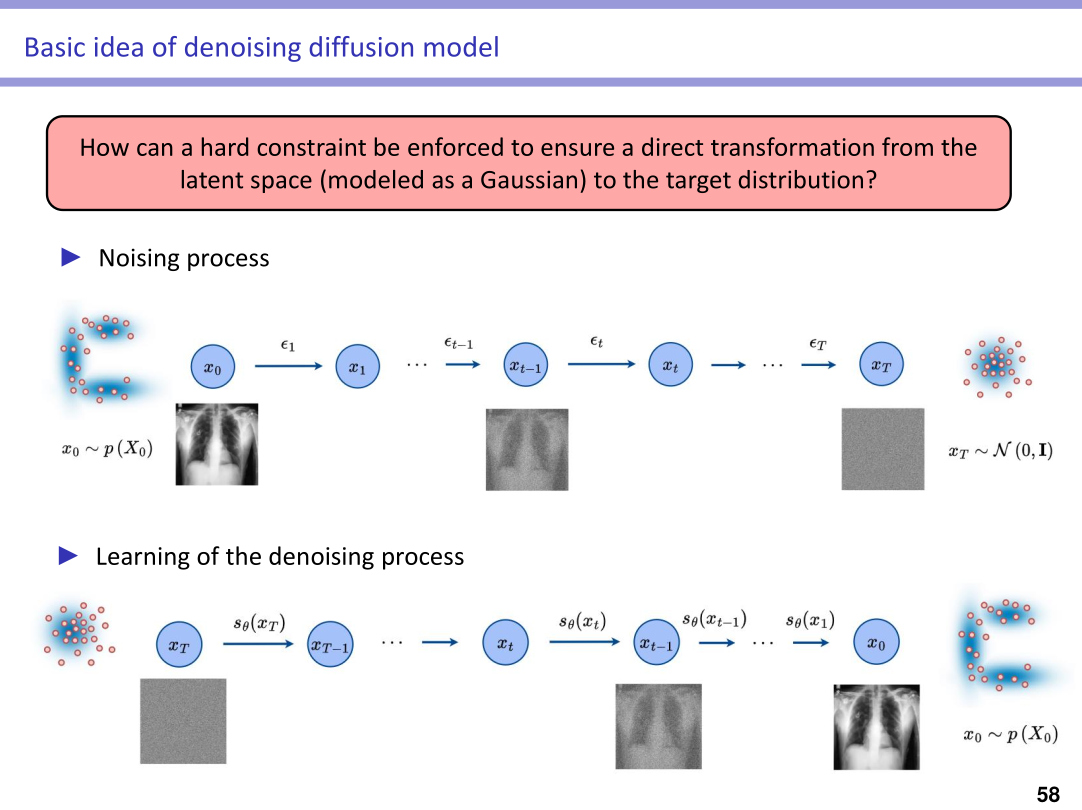
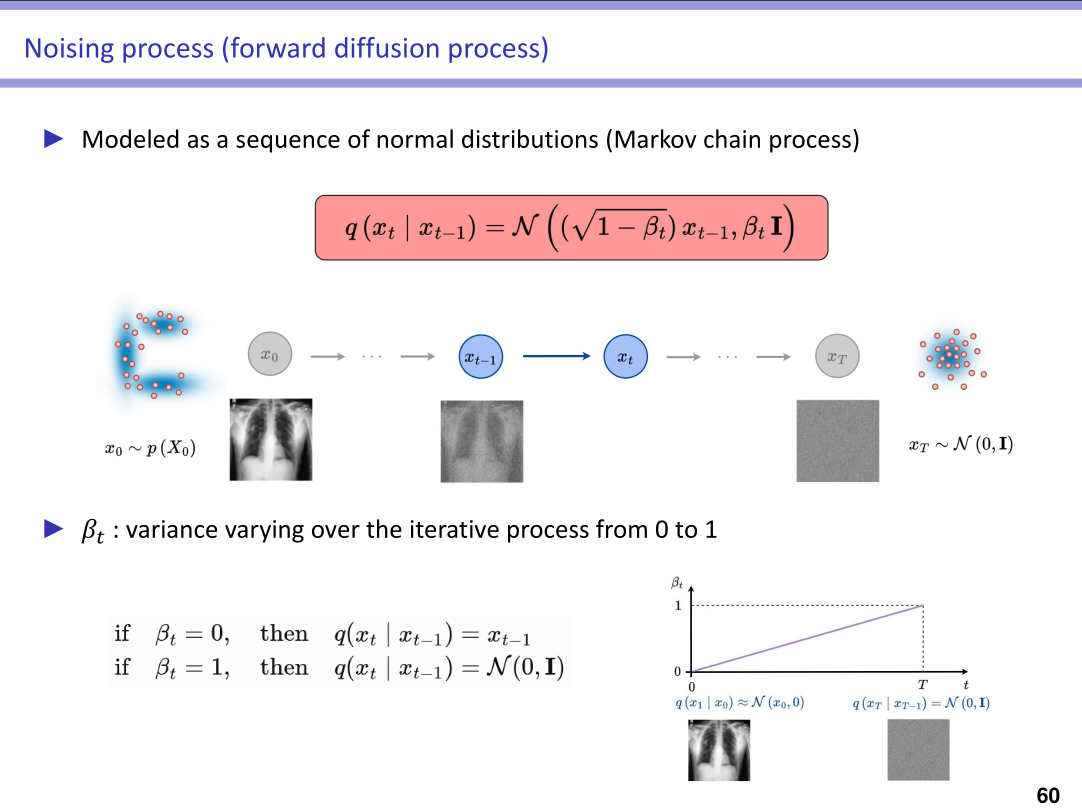
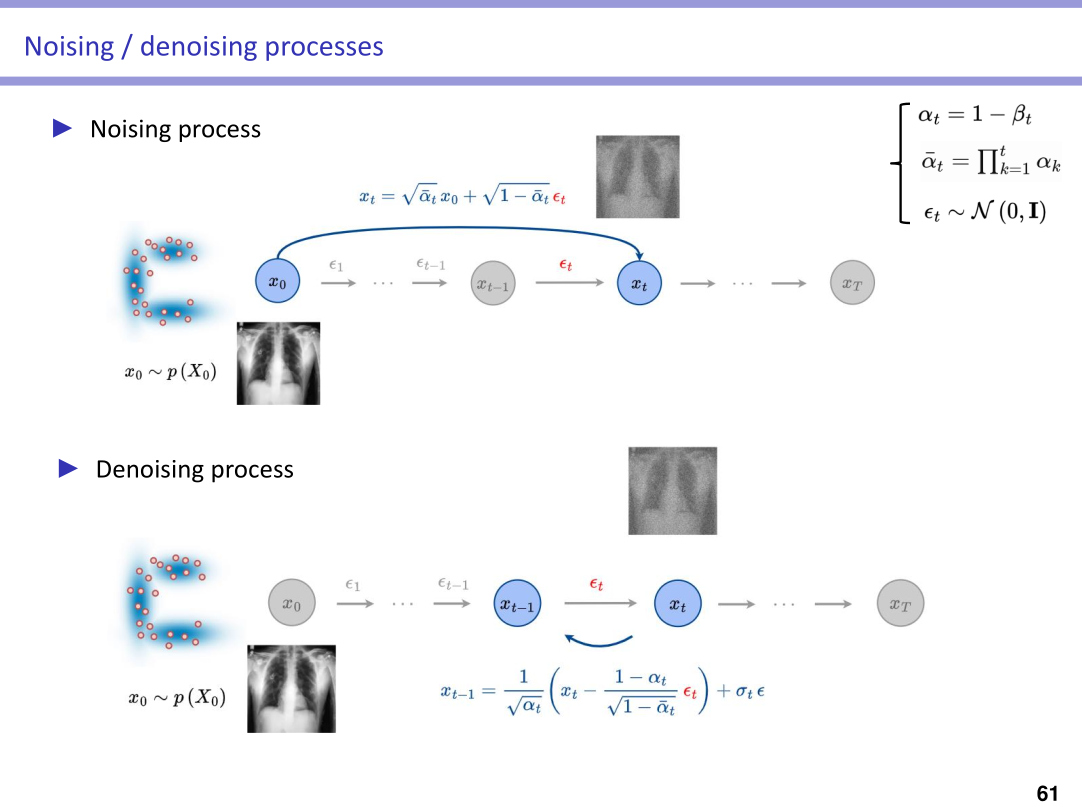
Highlights

  • Extending the idea proposed in the THOR method 1 to the training procedure
  • Learning to remove regions with anomalies of varying sizes using a diffusion process
  • Evaluation on three public datasets: IXI Dataset (brain MRI scans from approximately 600 healthy subjects), ATLAS 2.0 (655 T1-weighted MRI scans accompanied by expert-segmented lesion masks), and BraTS'21 (1251 brain scans across four modalities: T1-weighted, contrast-enhanced T1-weighted - T1CE, T2-weighted, and T2 Fluid Attenuated Inversion Recovery - FLAIR)

Motivations

  • Removing the need for forward and reverse processes in diffusion-based anomaly detection avoids several limitations, including feature degradation during forward diffusion and a trade-off between localization accuracy and removable anomaly size.

Overall idea

  • The method is based on the following hypothesis: starting from a VAE trained exclusively on normal subjects, a region containing abnormalities is efficiently represented as noise in the corresponding latent space.
  • Using a dataset of healthy subjects, relevant synthetic anomalies can be introduced by adding Gaussian noise of varying intensity to randomly selected regions via a forward diffusion process, and subsequently learning to remove them through a reverse diffusion process.

Key ideas

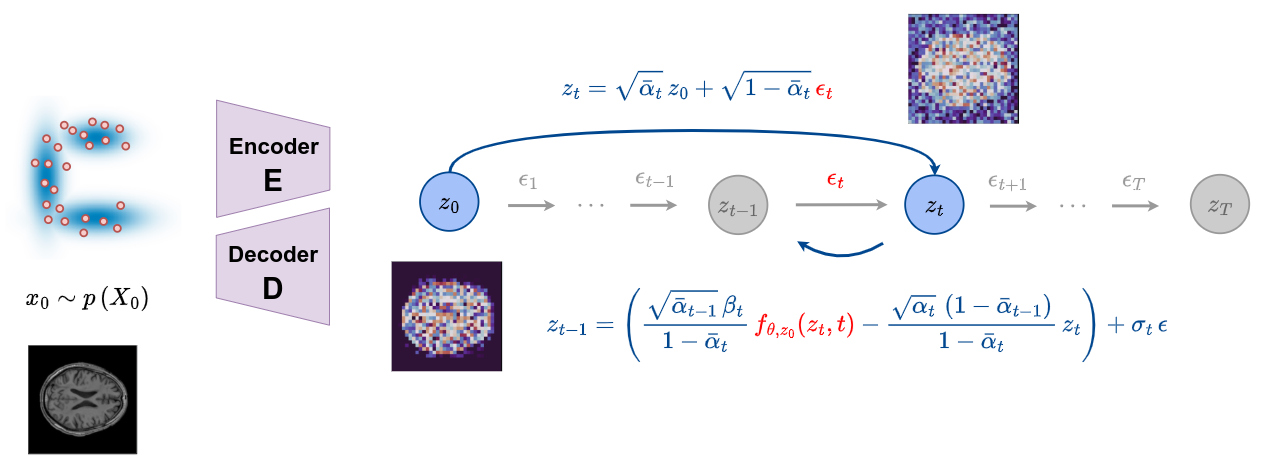
  • The diffusion process can be revisited by estimating \(x_0\), denoted as \(\hat{x}_0\), at any time step \(t\) using the following equations.

DDPM

  • Computation of the estimated \(\hat{x}_0(x_t,t)\) from \(\epsilon_\theta(x_t,t)\)
\[\color{red}{\hat{x}_0(x_t,t) = \frac{1}{\sqrt{\bar{\alpha}_t}} \left(x_t - \sqrt{1-\bar{\alpha}_t}\, \epsilon_\theta(x_t,t) \right)}\]
  • Computation of \(\epsilon_\theta(x_t,t)\) from the estimated \(\hat{x}_0(x_t,t)\)
\[\epsilon_\theta(x_t,t) = \frac{x_t - \sqrt{\bar{\alpha}_t}\,\hat{x}_0(x_t,t)} {\sqrt{1-\bar{\alpha}_t}}\]
  • The reverse process that links \(x_{t-1}\) with \(x_t\) can be rewritten as:
\[x_{t-1} = \left(\frac{\sqrt{\bar{\alpha}_{t-1}}\,\beta_t}{1-\bar{\alpha}_t}\,\hat{x}_0 + \frac{\sqrt{\alpha_t}\left(1-\bar{\alpha}_{t-1}\right)}{1-\bar{\alpha}_t}\,x_t\right) + \sigma_t \, \epsilon\]

DDIM

  • DDIM is commonly used to reconstruct images through a deterministic sampling process
  • The following DDIM expression is always true:
\[x_{t-1} = \sqrt{\bar{\alpha}_{t-1}}\,\hat{x}_0 + \sqrt{1-\bar{\alpha}_{t-1}}\,\epsilon_\theta\]
  • Using the relation that links \(\epsilon_{\theta}\) with \(\hat{x}_0\), this expression can be rewritten as:
\[\color{red}{x_{t-1} = \sqrt{\bar{\alpha}_{t-1}}\,\hat{x}_0 + \sqrt{1-\bar{\alpha}_{t-1}}\, \left(\frac{x_t-\sqrt{\bar{\alpha}_t}\,\hat{x}_0} {\sqrt{1-\bar{\alpha}_t}}\right)}\]

Methodology

Training procedure

Modeling the normal feature space

  • Exclusively healthy subjects are used during training: \(\{x^{(i)}\}_{i=1}^{N}\) with \(x^{(i)} \in \mathbb{R}^{H \times W \times C}\)
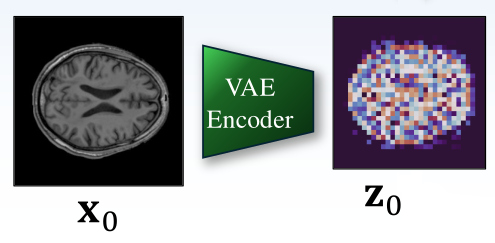
  • A pre-trained variational auto-encoder \(V_{E,\phi}\) is fine-tuned on the dataset and then frozen for the rest of the process
  • Each input image \(x^{(i)}\) are mapped to its latent space representation \(z^{(i)} = V_{E,\phi}\left(x^{(i)}\right)\), where \(z^{(i)} \in \mathbb{R}^{H' \times W' \times C'}\)

 

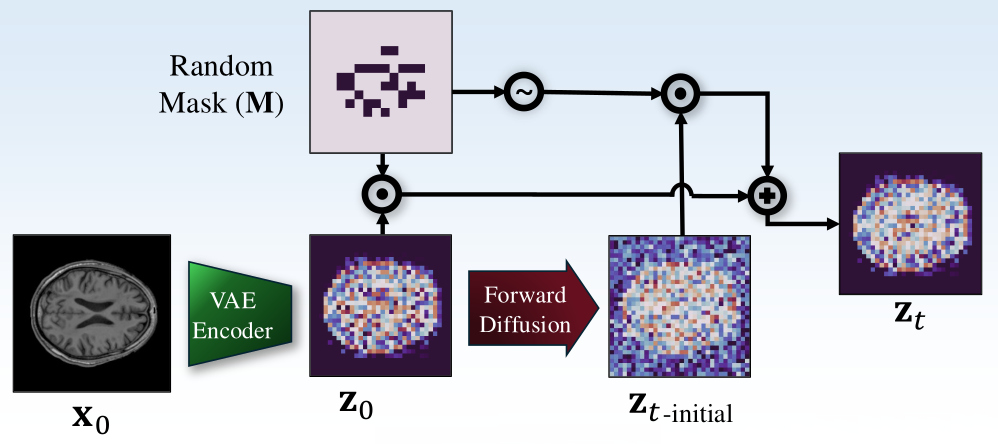
Random masking

  • The latent features of a normal input sample \(z_0\) are spatially partitioned into non-overlapping patches using a random mask \(M \in [0,1]^{H' \times W'}\)
  • This random mask simulates regions with abnormalities

Forward process

  • The forward diffusion process gradually applies noise to the masked patches of sample \(z_0\) for \(t\) time steps to generate samples \(z_t\) with \(t \in [1, T]\)

    \(z_t = \left( \sqrt{\bar{\alpha_t}} \, z_0 + \sqrt{1-\bar{\alpha_t}} \, \epsilon_t \right) \odot M + z_0 \odot \left( 1 - M \right)\)

    where \(\epsilon_t \sim \mathcal{N}(0,I)\), \(\alpha_t = 1 - \beta_t\) and \(\bar{\alpha_t} = \prod_{i=1}^{T} \alpha_i\)

 

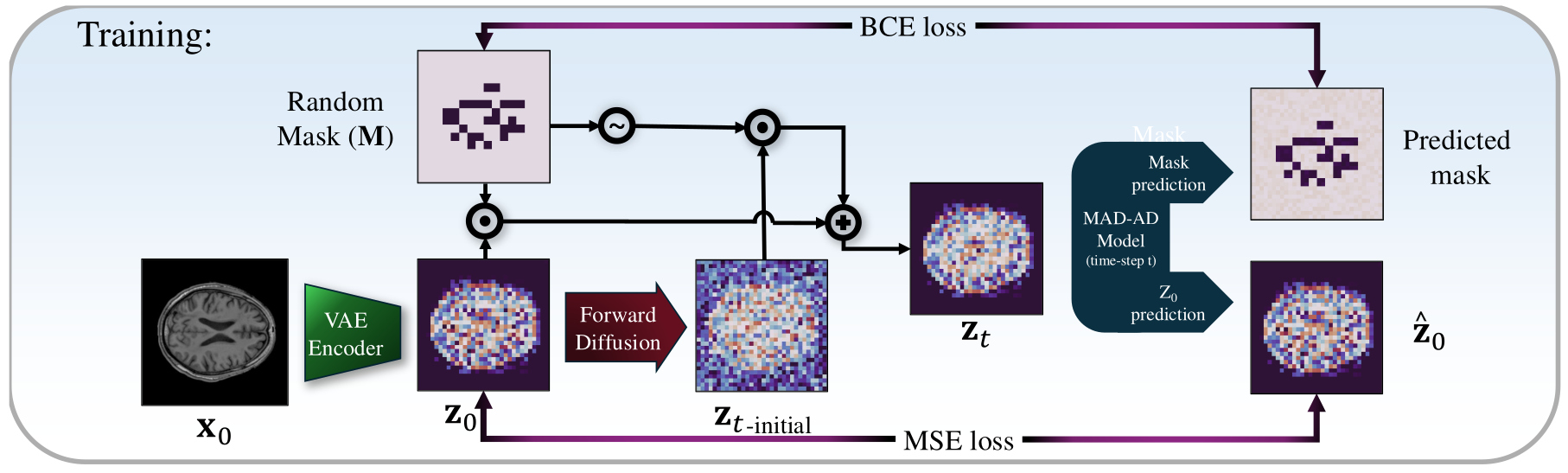
Reverse process

  • The reverse process aims to recover the original data \(z_0\) by gradually removing the noise
  • Given the sample \(z_t\) at step \(t\) and mask \(M\) at spatial location \(k\), the reverse process can be modeled as:
    \(p\left(z^k_{t-1} \mid z^k_t\right) = \begin{cases} \mathcal{N}\left( \mu_{\theta}(z^k_t,t), \, \beta_t \mathbf{I} \right), &\textit{if } M^k=1 \\ z^k_t, & \textit{otherwise} \end{cases}\)

    \(\mu_{\theta}(z_t,t)\) is a trainable function, which can be reparameterized as a predicted noise \(\epsilon\) or a predicted clean image \(z_0\)

  • Due to the incorporated random masking strategy, the predicted clean image formulation is chosen:

    \(\mu_{\theta}(z_t,t) = \frac{\sqrt{\bar{\alpha}_{t-1}} \, \beta_t}{1-\bar{\alpha}_t} \, \color{red}{f_{\theta,z_0}(z_t,t)} + \frac{\sqrt{\alpha_t}\,(1-\bar{\alpha}_{t-1})}{1-\bar{\alpha}_t} \, z_t\)

    where \(f_{\theta,z_0}(z_t,t)\) is a trainable function that predicts \(\hat{z}_0\) at time \(t\), given \(z_t\).

  • The following scheme is applied only to the masked region:
  • \(f_{\theta,z_0}\) is a neural network that is trained using a simple mean-square error loss between \(z_0\) and the predicted image without any noise:
\[\displaystyle \min_{\theta} \; \mathbb{E}_{z_0 \sim q(z_0),\, \epsilon,\, t} \left[ \left\| z_0 - f_{\theta, z_0}(z_t, t) \right\|_2^2\right]\]

Mask prediction

  • The location of the anomalous regions needs to be estimated during inference
  • An additional head \(f_{\theta,M}\) is added to the diffusion model to predict the mask used in the forward diffusion process

  • The final loss function is given as: \(\displaystyle \min_{\theta} \; \mathbb{E}_{z_0 \sim q(z_0),\, \epsilon,\, t} \left[ \left\| z_0 - f_{\theta, z_0}(z_t, t) \right\|_2^2\right] + \lambda \, \mathcal{L}_{\mathrm{BCE}}\!\left(M, f_{\theta, M}(z_t, t)\right)\)

    where \(\lambda\) is a hyper-parameter that balances the contributions of the two terms

Inference

Recovering normal images

  • Let \(\{ x'^{(i)} \}_{i=1}^N\) denote the test set at inference time, which consists of samples with potential anomalies
  • These images are first map into the latent space using \(V_{E,\phi}\)

The latent space of an anomalous image is treated as step \(T\) of a masked forward diffusion process applied on its normal counterpart, i.e., \(z'_T = V_{E,\phi}(x'_T)\)

  • By predicting the mask that corresponds to the anomaly location and the reconstructed \(\hat{z}'_0\) at each time-step \(t\), using the expression of \(p(z^k_{t-1} \mid z^k_t)\), it is possible to progressively correct the anomaly regions and obtain the normal counterpart \((z'_T \rightarrow z'_0)\) while preserving fine details of the normal regions  

  • One drawback of sampling with DDPM is that it requires many reverse sampling steps to obtain the normal version
  • A DDIM framework is used instead to make the reverse process more deterministic and require fewer sampling steps
  • The reverse process of DDIM is modified for the MAD-AD model as:

    \(\begin{aligned} \tilde{z}'_{t-1} &= \underbrace{B\!\left(\color{red}{f_{\theta,M}(z'_t)}\right)}_{\text{predicted mask}} \Big( \sqrt{\bar{\alpha}_{t-1}}\, \underbrace{\color{red}{f_{\theta,z_0}(z'_t)}}_{\text{predicted } \hat{z}'_0} + \underbrace{\sqrt{1 - \bar{\alpha}_{t-1}}\, \color{red}{\hat{\epsilon}_t(z'_t)}}_{\text{direction pointing to } z'_t} + \sigma_t \epsilon'_t \Big) \\ &\quad + \left( 1 - B\!\left(\color{red}{f_{\theta,M}(z'_t)}\right) \right) z'_t \end{aligned}\)

    where \(\hat{\epsilon}_t(z'_t) = \frac{z'_t - \sqrt{\bar{\alpha}_t}\,\color{red}{f_{\theta,z_0}}(z'_t)} {\sqrt{1-\bar{\alpha}_t}}\)

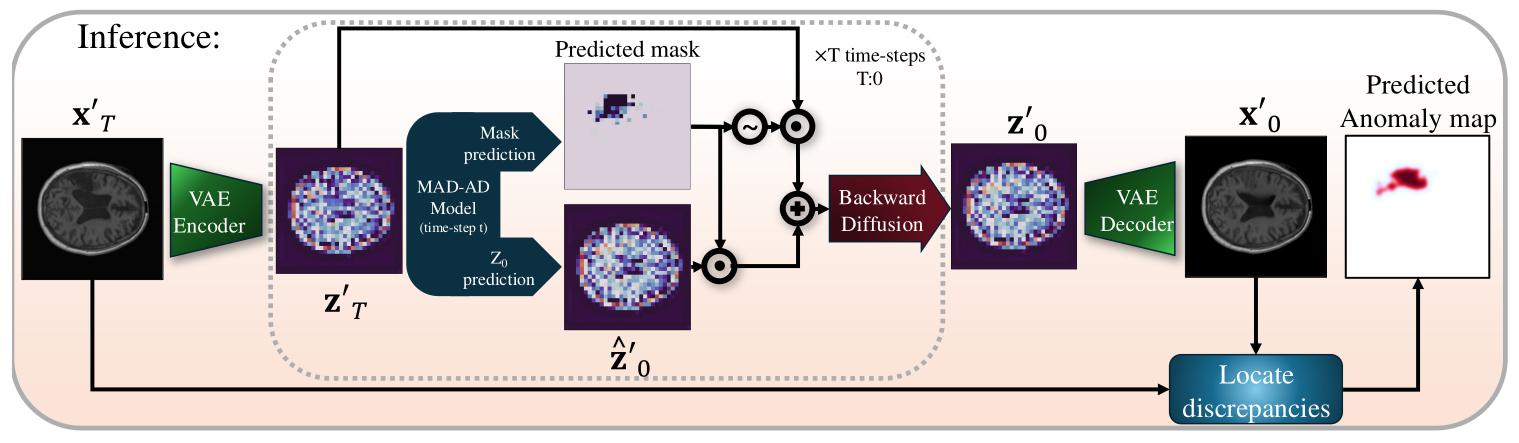
Anomaly localization

  • The discrepancy between the input image and its reconstructed normal counterpart is used to localize anomalies
  • Using the normal latent embedding \(\hat{z}'_0\), the normal sample is reconstructed in the image-space as: \(\hat{x}'_0 = V_{D,\phi}(\hat{z}'_0)\), where \(V_{D,\phi}\) is the pre-trained VAE decoder
  • The predicted anomaly map is then given by

    \(a = G * \min \left( \left\| \hat{x}'_0 - x'_0\right\|_2^2, \gamma \right) / \gamma\)

    where \(G\) is a Gaussian kernel to smooth the predicted mask, \(∗\) is the convolution operator, and \(\gamma\) is a threshold designed to prevent assigning excessive weight to patches with significant deviations

Experiments

  • The Maximum Dice score, which reports the highest value obtained for thresholds ranging from 0 to 1, is used to evaluate the performance of the anomaly detection model.
  • A pre-trained VAE with perceptual loss and patch-based adversarial objective is used to project the data into a latent space, reducing the spatial dimension by a factor of 8
  • The diffusion model corresponds to a standard UNet with attention
  • The number of training and inference time-step (\(T\)) is set to 10
  • To form the random mask at each iteration, the masking ratio is drawn from a uniform distribution \(U [0, 0.4]\), and the patch sizes of the mask along the \(X\) and \(Y\) axes are sampled independently from the following set: \(\{1, 2, 4, 8\}\)
  • The random mask is then multiplied by the brain mask to prevent noise in non-brain
  • The model was trained for 300 epochs using a batch size of \(96\) and AdamW optimizer with a learning rate of \(5 × 10^{−4}\)

Results

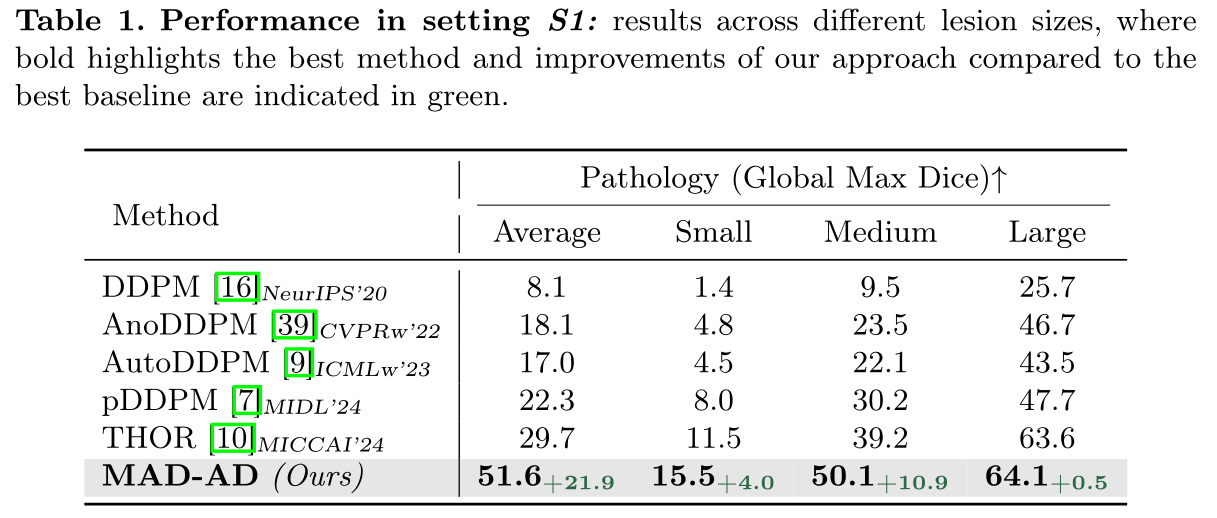
Setting-1 (S1)

  • Training is performed on the middle slices of IXI dataset, whereas only middle slices of ATLAS 2.0 are used for testing

 

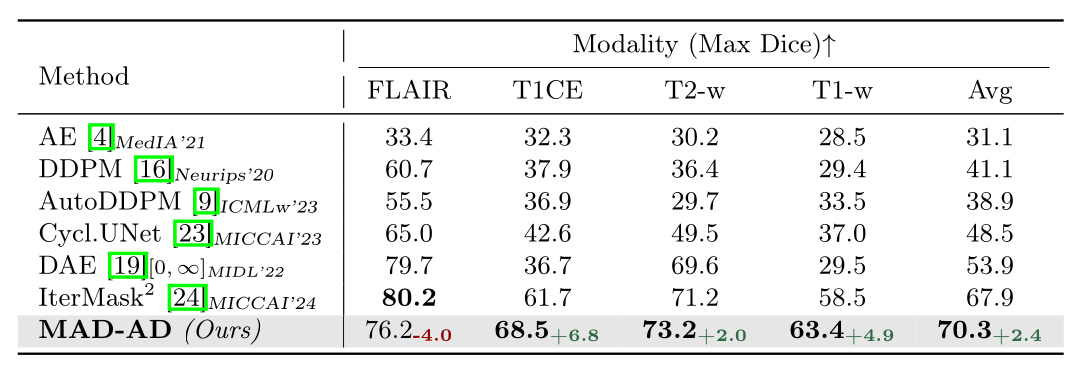
Setting-2 (S2)

  • BRATS’21 dataset is used. Normal slices are used for training, while the abnormal slice with the largest pathology is employed for inference.

 

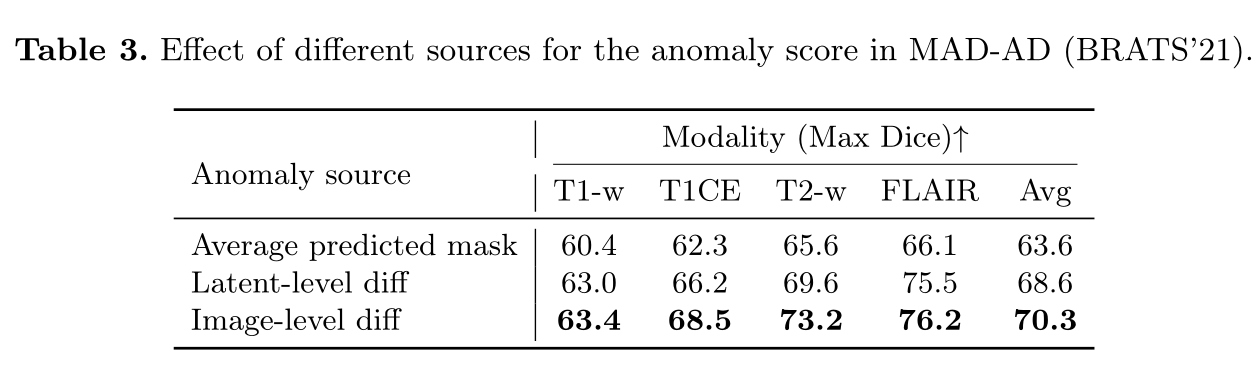
Ablation study

  • Comparison of different strategies to form the anomaly map: pixel-level discrepancies \((x'_0,x'_T)\), latent-space discrepancies \((z'_0,z'_T)\), and the average of the predicted mask at reverse diffusion steps \(\frac{1}{T}\sum_{t=1}^T f_{\theta,M}(z'_t)\)

 

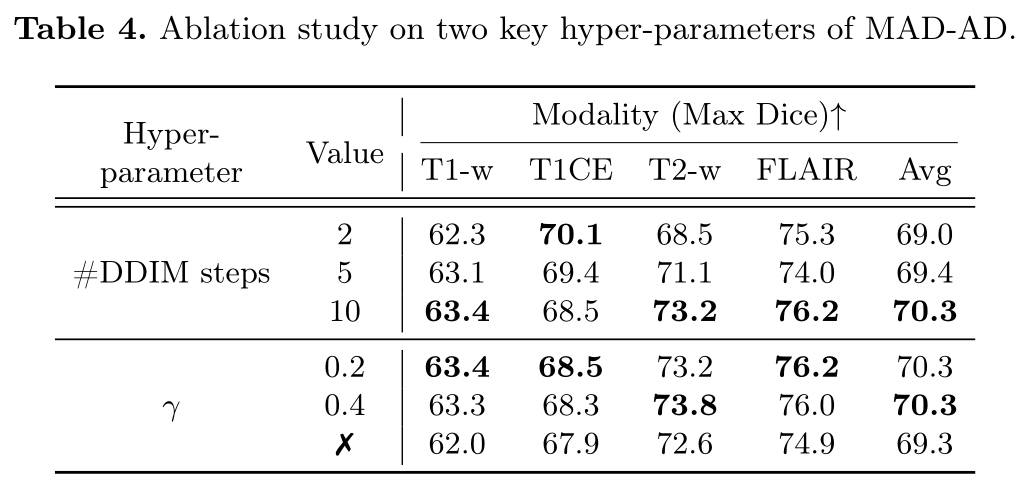
  • Evaluation of the influence of key hyper-parameters on the performance of the proposed method

 

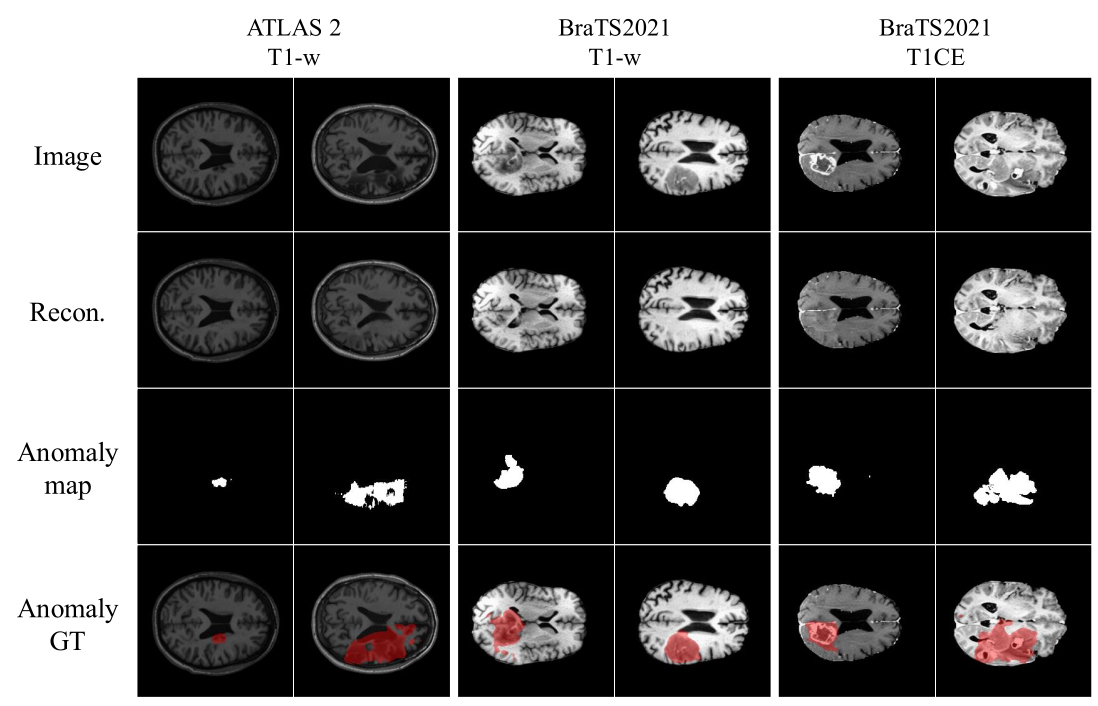
Qualitative results

Conclusions

  • This paper presents an unsupervised anomaly detection
  • The originality of the method is to introduce a unified formalism for forward and reverse diffusion processes applied consistently during training and inference
  • The method beats state-of-the-art methods on two different settings involving three different datasets

Reference

  1. Cosmin I. Bercea, Benedikt Wiestler, Daniel Rueckert, and Julia A. Schnabel. Diffusion Models with Implicit Guidance for Medical Anomaly Detection., MICCAI 2024 ↩