Raptor: Scalable Train-Free Embeddings for 3D Medical Volumes Leveraging Pretrained 2D Foundation Models
Highlights
- Raptor (Random Planar Tensor Reduction) is able to leverage a pretrained image model to create and compress visual tokens in 3D.
- Achieves state-of-the-art performance across 10 medical volume tasks without the need for costly training.
- The method is straightforward and easy to understand.
- It is easy to reimplement yourself or use the existing code.
Introduction
Understanding and processing volumetric data is essential in a variety of applications, including healthcare (e.g. brain MRIs, chest CT images).
-
Following the emergence of foundation models for natural images, such as DINO [^1] and SAM [^2], the development of analogous models for medical imaging has become a highly compelling research direction [^3].
-
Current challenges stem from the computational complexity of training sota architectures in high dimensions and curating sufficiently large datasets of volumes.
-
Raptor is a train-free method for generating semantically rich embeddings for volumetric data, leveraging a frozen 2D foundation model pretrained on natural images, significantly reducing computational complexity and cost.
-
Experiments on ten medical volume tasks verify the superior performance of Raptor over sota methods, including those pretrained exclusively on medical volumes.
Note: an image foundation model is a large-scale vision model pretrained on vast image datasets—typically using self-supervised learning—to learn general, transferable visual representations (embeddings) that can be adapted to many downstream tasks such as classification, detection, or segmentation with fine-tuning.
Method
Raptor is an efficient low-rank approximation of the high-dimensional tensor inferred by the DINOv2-L ViT. This is achieved through mean pooling across slice embeddings and random projections. This approach requires no additional training of parametric models.
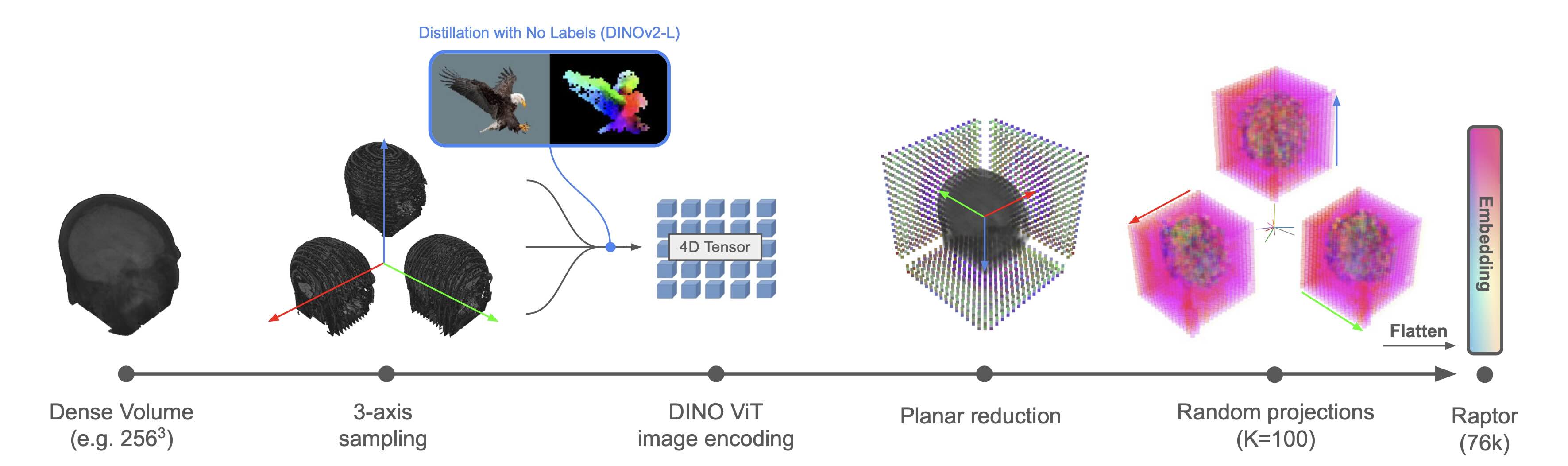
ViT feature extraction. A volume \(x \in \mathbb{R}^{D \times D \times D}\) can be decomposed into 2D slices (\(S_i\)) along each of the three orthogonal directions (axial, coronal, and sagittal). A pretrained ViT \(\phi(\cdot)\) is applied across the 3D volume along all three axes to obtain intermediate representations:
\[z = \operatorname{concat}_{1 \le i \le 3} [\phi(S_i)] \in \mathbb{R}^{3 \times D \times d \times p^2}\]- \(d\) = token dimension
- \(T\) = ViT patch size
- \(p = D/T\) = number of patches per spatial dimension
Mean pooling across slices. \(z\) is reduced by averaging over the slice dimension:
\[\tilde{z}_i = \frac{1}{D} \sum_{j=1}^{D} z_{ij}\]Repeating this for all three directions produces a tensor of size \(3 \times d \times p^2.\)
Random projection. For each of the \(p^2\) patches, a low-rank approximation is computed using random projections. A projection matrix is sampled: \(R \in \mathbb{R}^{K \times d}, \quad R_{kl} \sim \mathcal{N}(0,1),\) where \(K d\). Projecting the tokens yields a tensor of size \(3 \times K \times p^2.\)
The Raptor embedding in one formula. The final Raptor embedding is obtained by flattening:
\[v = \operatorname{flatten} \left( \operatorname{concat}_{1 \le i \le 3} \left[ R \left( \frac{1}{D} \sum_{j=1}^{D} z_{ij} \right) \right] \right) \in \mathbb{R}^{3 K p^2}.\]Here, \(j\) indexes slices along axis \(i\). The size of Raptor embeddings scales as \(\mathcal{O}(p^2 K)\), which is sub-cubic in the dimension of the input volume.
Typical Settings
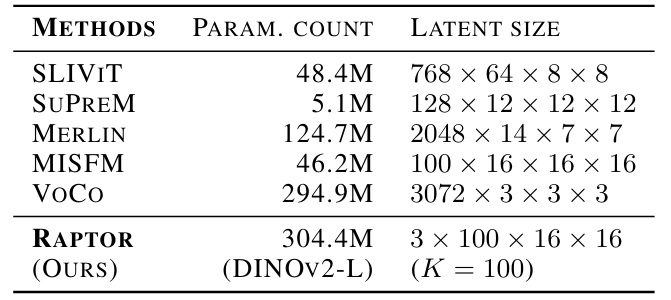
The authors chose to use DINOv2-L encoder (304M parameters) which trained ViT on a curated dataset of 142M 2D natural images (LVD-142M) and 1.2B additional images crawled on the web. Keep in mind that method is agnostic of the model. They used the following settings:
- \(D =\) 256
- \(d =\) 1024
- \(T =\) 16
- \(p = D/T = 256/16 =\) 16
This results in Raptor embeddings of size:
\[3 \times 16^2 \times K = 768K.\]The authors compute two variants:
- Raptor with \(K = 100\)
- Raptor-B (Base) with \(K = 10\)
Note: the random projection is chosen over other methods (e.g. PCA) for time complexity reasons. About the effectiveness of random projections, the Johnson–Lindenstrauss lemma states that distances between points (e.g., patch embeddings) are preserved up to a small distortion factor (1 ± \(\epsilon\)) with high probability when mapped into \(\mathbb{R}^K\).
Experiments
The authors compare methods on classification (metrics: AUROC and accuracy) and regression (metrics: Pearson’s \(r^2\)) tasks.
For Raptor embeddings, they train logistic regression models for classification tasks, and MLPs under an MSE loss for regression tasks.
Hyperparameter tuning (L2 regularization, MPL layers) on validation set and final results on test set.
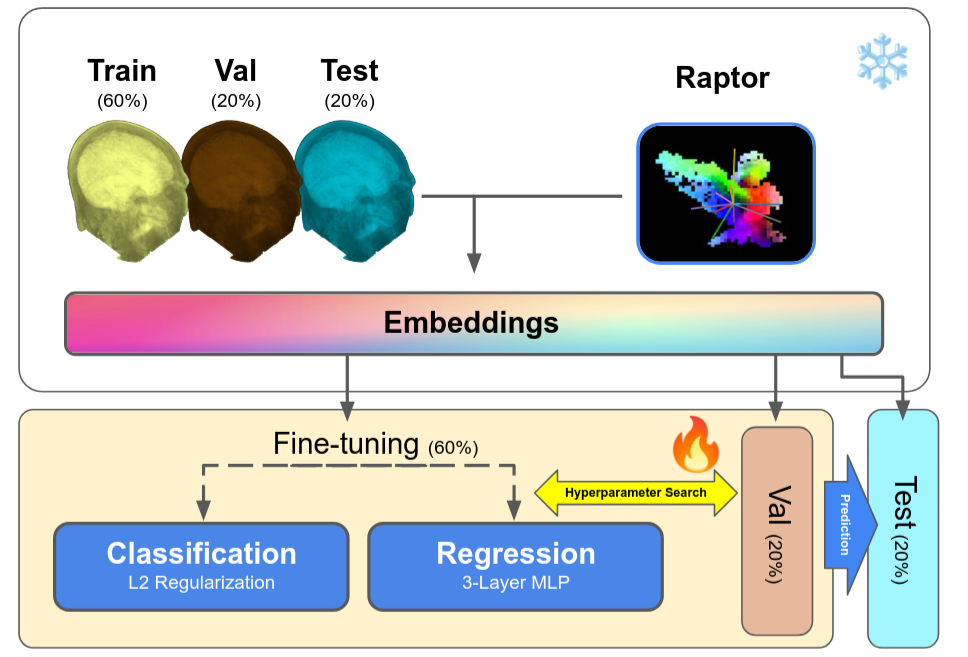
The other methods are fully fine-tuned. For models which do not have a classification or regression head, they add a single linear layer above their latent space.
Datasets
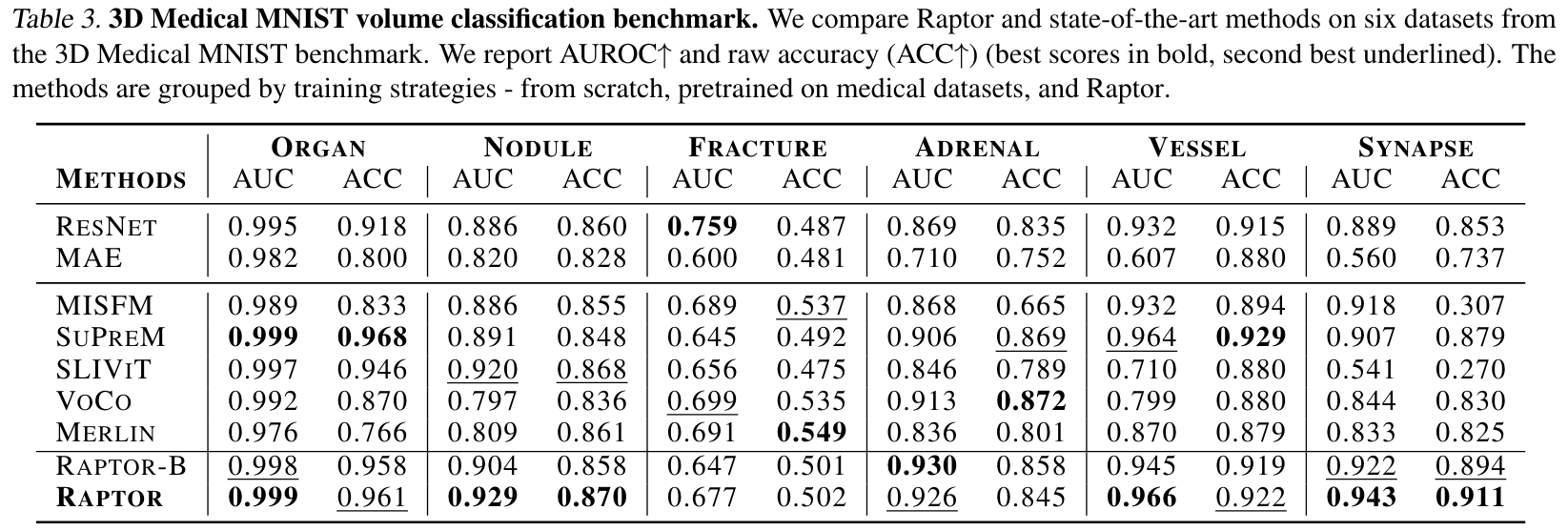
- 3D Medical MNIST: includes 6 separated classification tasks on CT and MRI, from 2 to 11 classes, with no more than 1.3k images per dataset.
- CC-CCII: 2,471 chest CT scans, 3 classes.
- CTRG: 6,000 brain MRIs for 3 classes (CTRG-B) and 1,804 chest CTs for 4 classes (CTRG-C).
- UKBB Brain MRIs: 1,476 MRIs with multiple regression targets per MRI, corresponding to imaging-derived phenotypes (IDPs) averaged in 10 major brain regions.
Other methods
- Baselines. A 3D ResNet-50 and a 3D ViT. For each dataset, the ViT is pretrained with MAE.
- Pretrained medical models.

Results
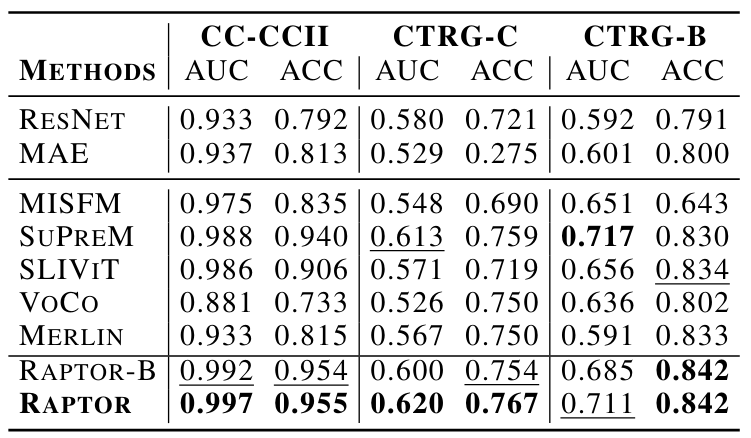
Classification:
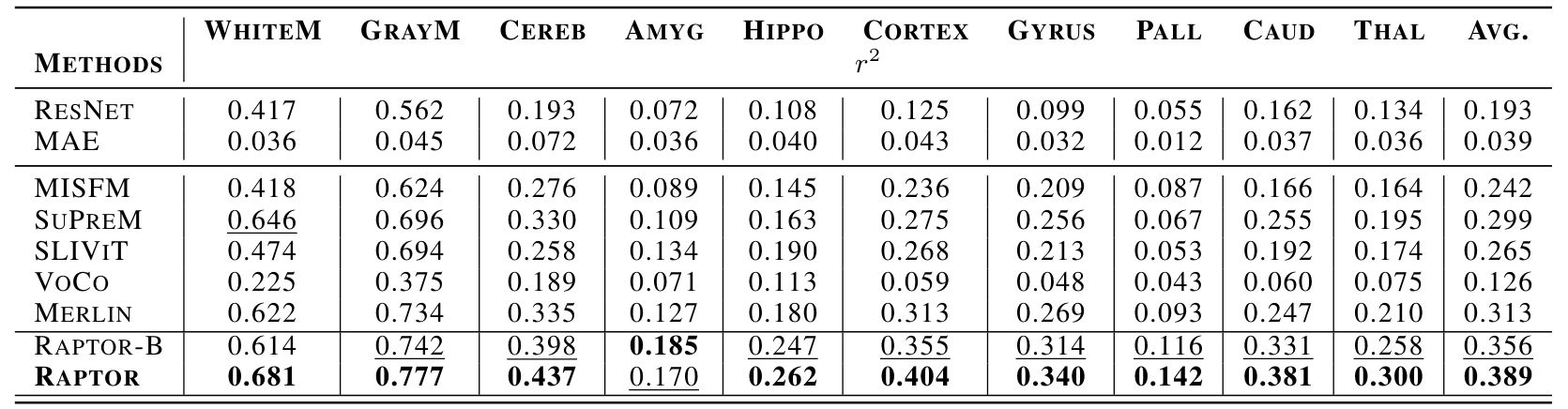
Regression on brain volumes:
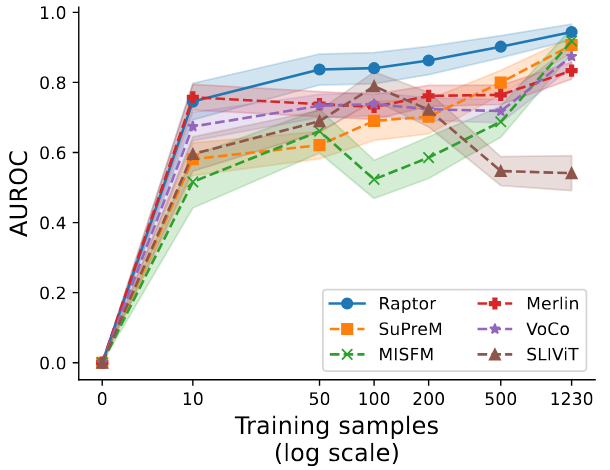
Effectiveness in data-constrained settings on the Synapse dataset (from 3D Medical MNIST):
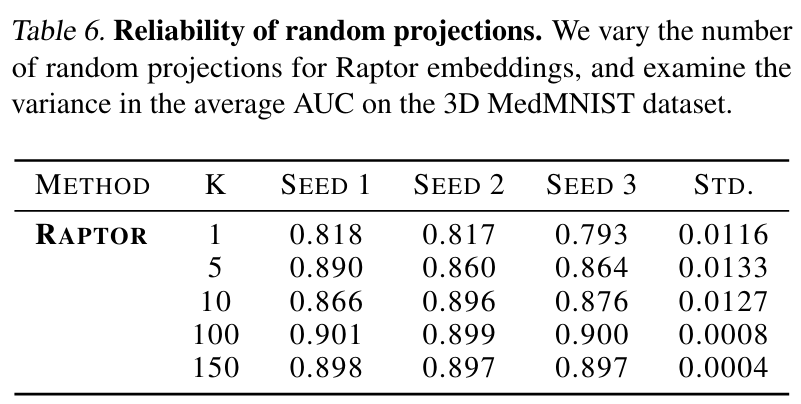
Ablation studies
Influence of \(K\):
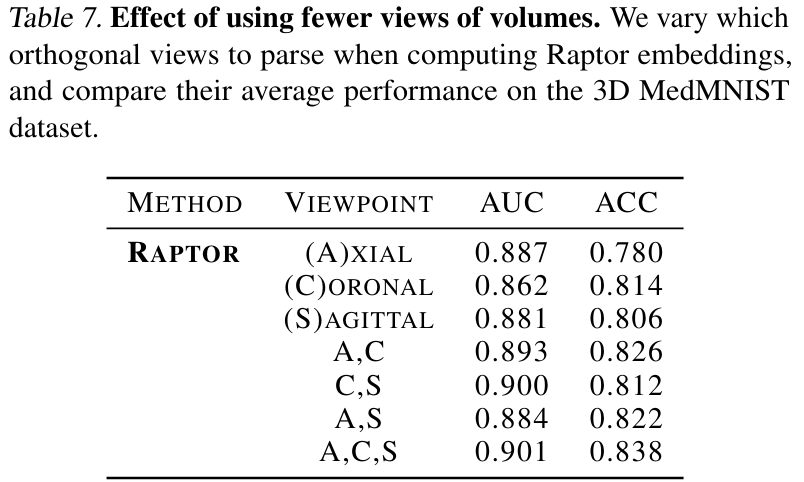
Influence of selected axis:
Limitation on detectable features:
Explore the spatial sensitivity and resolution limits of the method.
In the Location task, the same MNIST digit is embedded in two volumes, at varying lateral pixel (px) distances (64px to 8px). The authors test whether Raptor can distinguish the two.
In the Size task, a MNIST digit of varying sizes (from 64px to 8px) is randomly inserted into the volumes. the authors test whether Raptor can detect the presence of the digit.
For both tasks, binary classifiers are trained on top of the Raptor embeddings.

Conclusion
- Raptor achieves sota performance across a range of medical imaging tasks.
- Compress volumes into a representation space significantly smaller than those used in prior works.
- Underscore the efficacy of Raptor as a paradigm-shifting framework for volumetric data analysis that overcomes major challenges in the field by leveraging pretrained 2D foundation models.
- Scalable and generalizable solution for resource-constrained settings.
- Domain-specific priors or refining the axial sampling strategy could further improve downstream results
- Hold promise for broader applications, including multimodal integration and large-scale analysis of medical data.
References
[^1] M. Caron et al., “Emerging Properties in Self-Supervised Vision Transformers,” 2021 IEEE/CVF International Conference on Computer Vision (ICCV), Montreal, QC, Canada, 2021, pp. 9630-9640, doi: 10.1109/ICCV48922.2021.00951.
[^2] A. Kirillov et al., “Segment Anything,” 2023 IEEE/CVF International Conference on Computer Vision (ICCV), Paris, France, 2023, pp. 3992-4003, doi: 10.1109/ICCV51070.2023.00371.
[^3] E. Kaczmarek, J. Szeto, B. Nichyporuk, and T. Arbel, “Building a General SimCLR Self-Supervised Foundation Model Across Neurological Diseases to Advance 3D Brain MRI Diagnoses”.