Highlights

The authors proposes a new type of convolution, called Fast Fourier Convolution (FCC), that allows to convey local and global information by taking advantage of 2D-Fourier Transform’s global receptive field.
Replacing classic convolutions with fast Fourier convolution in backbones increases accuracy on several standard vision tasks.
Code is available on the official GitHub page.

Introduction

A majority of modern networks have adopted the architecture of deeply stacking many convolutions with small receptive field, commonly of size 3x3. The receptive field of such model grows as the information goes deeper into the network. However, it has been showed that increasing the receptive field, for instance though deformable convolution¹ or non-local neural networks², could enhance the performances of convolutional models. Moreover, gathering and exploiting information at different scales has also proven to be effective in refining local spatial detection by integrating information from shallower layers.

To tackle this challenge, the authors introduce a novel convolution operator that has a non-local receptive field and fuses multi-scale representations. It is based on spectral transform theory, and especially Fourier Transform³. The key point is that any change in a value of the original data has an influence on the spectral domain. Hence, convolutional operations performed in the spectral domain have a global receptive field. Standard convolution have already been employed for processing images directly in the spectral domain with deep learning, but here the main idea is to couple information both from local and global context via an hybrid convolution.

Fast Fourier Convolution

Let’s consider an input of a convolution layer \(X \in \mathbb{R}^{H \times W \times C}\) and split it along the features’ dimension : \(X = \left \lbrace X^{l}, X^{g} \right \rbrace\), with \(X^{l} \in \mathbb{R}^{H \times W \times (1-\alpha_{in})C}\) and \(X^{g} \in \mathbb{R}^{H \times W \times \alpha_{in}C}\). The ratio \(1-\alpha_{in}\) defines how many of the features will be dedicated to local operations via classic convolutions.

The output of the forward pass of a Fast Fourier Convolution is defined as follows (see Figure 1 for illustration) :

\[Y^{l} = Y^{l \rightarrow l} + Y^{g \rightarrow l} = f_{l}(X^{l}) + f_{g \rightarrow l}(X^{g}) \\ Y^{g} = Y^{g \rightarrow g} + Y^{l \rightarrow g} = f_{g}(X^{g}) + f_{l \rightarrow g}(X^{l})\]

where \(Y^{l} \in \mathbb{R}^{H \times W \times (1-\alpha_{out})C}\) and \(Y^{l} \in \mathbb{R}^{H \times W \times \alpha_{out}C}\). To simplify the hyperparameters’ tuning, the two ratios \(\alpha_{in}\) and \(\alpha_{out}\) are set equal.

\(f_{l}(\cdot)\) is aimed to capture small scale information and \(f_{g \rightarrow l}(\cdot)\) and \(f_{}(\cdot)\) serve to exchange information between local and global levels. These three components can be any regular convolutional blocks, for instance 3x3 Conv + BN + ReLU. The term \(f_{g}(\cdot)\), called spectral transformer, is operating at a global scale though Fourier transform, and needs to be further explained.

Figure 1. Architecture of a Fast Fourier Convolution.

Fourier Unit and Local Fourier Unit

Fourier Unit

The goal of the global path in the FFC is to enlarge the receptive field of the convolution to the full resolution of the input feature map. To do so, the input channels are passed to the spectral domain with a discrete Fourier transform. When aplying 2-D Fourier Transform on some real signals, it returns a Hermitian matrix, and convertly, applying inverse 2-D Fourier Transform on an Hermitian Matrix results in a matrix with only real elements. These two principles are used to ensure compatibily with other real neural layers, as well as allowing to retain only half on the information of the spectral signal.

In the spectral domain, the real and imaginary parts of the signal are concatenated and standard convolutions layers can be used on the new feature tensor. Since a change in any region of the image in the original space has an influence on the whole spectral domain, using 1x1 convolution after a Fourier transform is sufficient to have a global receptive field.

When all the desired operations are been carried out in the frequency domain, an inverse Fourier transformed is applied to return to the image space.

The figure 2 shows the pseudocode of the Fourier Unit implemented in this paper :

Figure 2. Pseudocode of a Fourier Unit.

Local Fourier Unit

The authors also create a semi-global unit in their convolutional pipeline with the Local Fourier Unit. The goal is to capture more information at an intermediate scale between classic local convolution and global spectral convolution. To do so, the features on the global branch (see Figure 1) is split again, with a quarter on the features being kept for this semi-global purpose. As shown in Figure 3, these features are spatially divided into 4 groups and concatenated along the features’ dimension. A Fourier Unit is applied to this new tensor, and its output is replicated 3 times to get back to the original shape and allow elementwise sum with the other tensors of the spectral transform layer.

The full principle of the spectral transforms is summarized in the following figure :

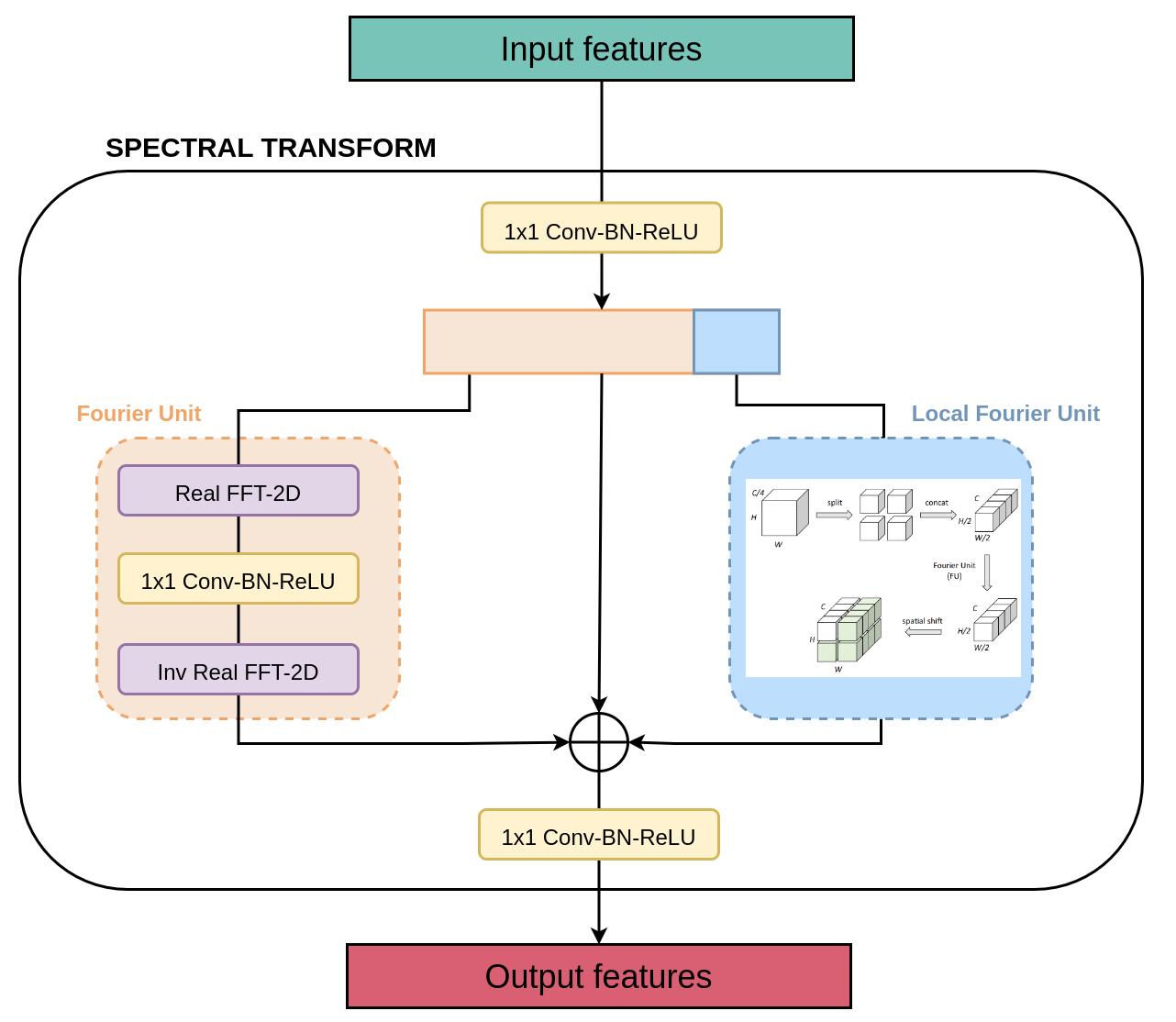
Figure 3. Illustration of the spectral transform performed in a FFC Block.

NOTE: Local Fourier Unit is adopted here by the authors as it slightly increases thhe performances when used in conjunction with the Fourier Unit. However, the main idea carried by the paper lies in the Fourier Unit and its global receptive field. In several other applications where the Fast Fourier Convolution is reemployed, the Local Fourier Unit is not retained.

Results

The efficiency of their convolution is assessed on some classic computer vision tasks. In those tests, the authors have replaced the standard convolutions in several backbones by their hybrid convolutional blocks. This change is done with a quite low computational cost, as it increases the number of parameters and FLOPs by only 2 to 5%.

The two figures below show the performances that they achieved on the ImageNet classification task and the Human Keypoint Detection on COCO.

Figure 4. Experiments results when plugging FCC into some networks on ImageNet.

Figure 5. Performances achieved on the COCO val2017 dataset for human keypoint detection.

The authors have carried out an ablation on the main hyperparameter of their convolution module, the split ratio between the features to the global et (semi-)global scale. The largest increase in performance appears when the new cross-scale mechanism is introduced (+1.0 point in accuracy), even at a low proportion. The study is conducted for a classification task and reveals that in that case the best split ratio is 0.5, although the conclusion could differ for another task, like segmentation.

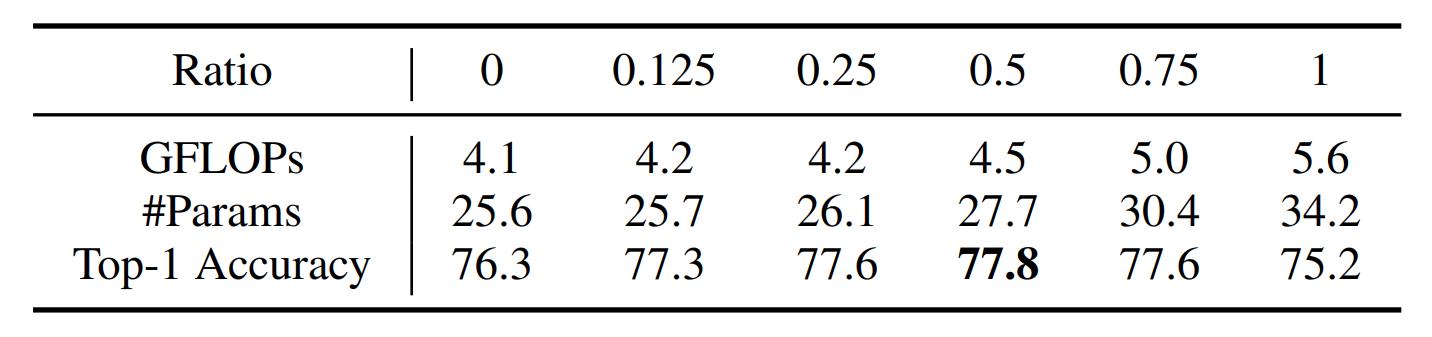
Figure 6. The top-1 accuracy of FFC under different ratios on ImageNet. All models use ResNet-50 as their backbones. Note that α = 0 is equal to using vanilla convolutions.

Additional results presented in the paper include further performances evaluation and an ablation study to demonstrate the relevance of the Local Fourier Unit, as well as the choice of this new module’s hyperparameter.

Conclusion

Fast Fourier Convolution is an alternative to standard spatial convolution that combines information at a local and global scale by taking advantage of Fourier transform to have a global receptive field. Replacing usual convolution with this hydrib one seems to be able to improve performances of CNNs at a small computational cost. It has been recently used in applications that benefit from global receptive fields, such as large mask inpainting⁴.