Notes

  • Link to the code here

 

Highlights

  • Extension of TreeVAE by adding a diffusion model
  • Controlling image synthesis based on learned clusters
  • Better reconstruction quality
  • Evaluation on MNIST, FashionMNIST, CIFAR-10, CelebA, and CUBICC (images of birds)

 

Overall idea

  • Two-stage framework
  • TreeVAE
    • Get a structured hierarchical latent representation (from root to leaf) from a TreeVAE
    • Process the nodes with a path encoder to create the conditioning signal
  • DDIM
    • Denoising Diffusion Implicit Model using the path encoder as conditioning to generate cluster-conditional samples

      In treeVAE, multiple decoders were used to reconstruct the images. Here, the DDIM serves as the reconstruction model

 

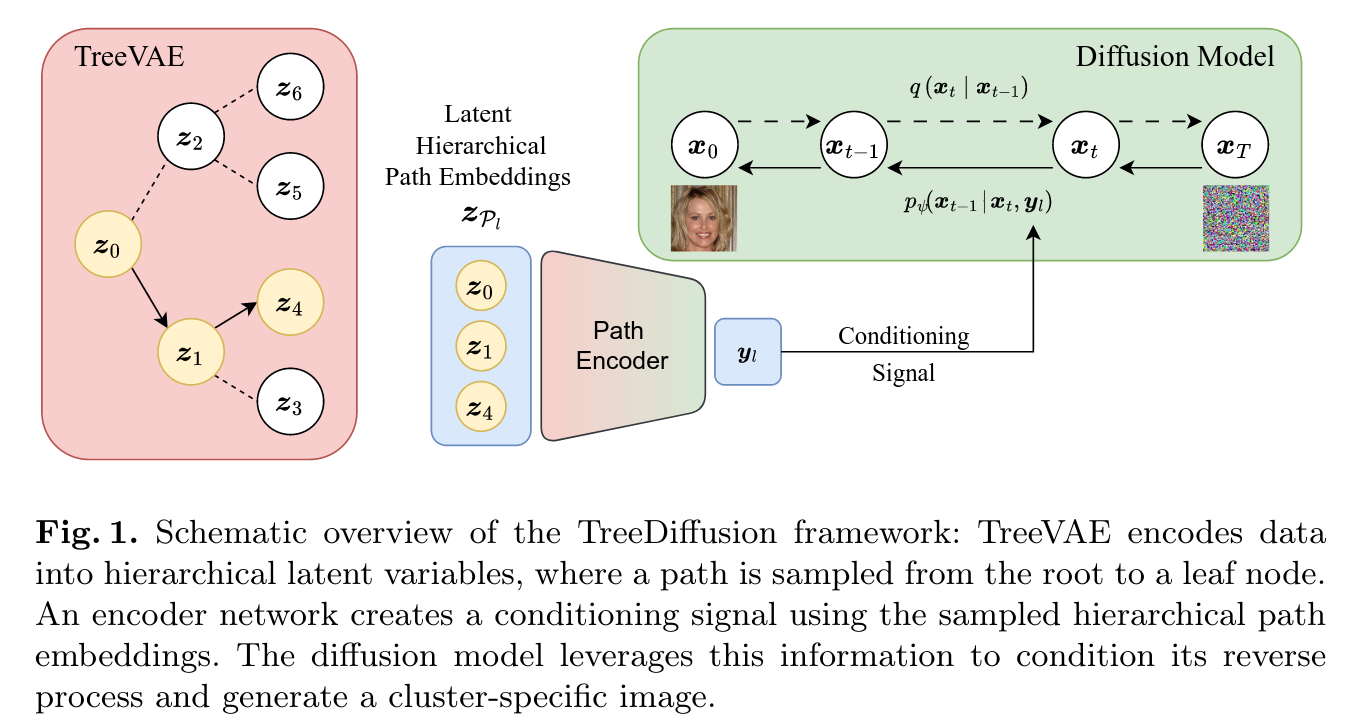
Methods

TreeVAE Reminder

  • The full post is available here
  • The network starts with a root and two child nodes and optimize the ELBO for a fixed number of epochs
  • Then it picks the leaf with the highest sample count and split it by adding two child nodes to promote balanced leaves
  • Unchanged parts are frozen and only the subtree formed by the new leaves are trained.

  • The processus alternates between expansion and localized training until reaching the target depth or number of leaves (hyperparameters)

  • \(\mathbb{V}\) represents the nodes of the tree
  • \(\textbf{z}_0,...,\textbf{z}_v\) are stochastic latent variables of each node
  • A given sample traverses the tree from root \(\textbf{z}_0\) to a leaf node \(\textbf{z}_l\)
  • The decisions of moving to either child node are \(c_i\) for each non-leaf node \(\textit{i}\). They follow a Bernoulli distribution, where \(c_i = 0\) corresponds to the left child
  • \(\mathcal{P}_l\) is the path or the sequence of nodes from the root to one leaf \(\textit{l}\)
  • \(z_{\mathcal{P}_l} = \left\{ z_i \mid i \in \mathcal{P}_l \right\}\) is the set of latent embeddings for each node in the path \(\mathcal{P}_l\)
  • The generative model is defined by :
\[p_\theta(z_{\mathcal{P}_l}, \mathcal{P}_l) = p(z_0) \prod_{i \in \mathcal{P}_l \setminus \{0\}} \underbrace{p\left(c_{\mathrm{pa}(i) \rightarrow i} \mid z_{\mathrm{pa}(i)}\right)}_{\text{decision probability}} \underbrace{p\left(z_i \mid z_{\mathrm{pa}(i)}\right)}_{\text{sample probability}}\]
  • The inference model is defined by :
\[q\left(z_{\mathcal{P}_l}, \mathcal{P}_l \mid x\right) = q\left(z_0 \mid x\right) \prod_{i \in \mathcal{P}_l \setminus \{0\}} q\left(c_{\mathrm{pa}(i) \rightarrow i} \mid x\right) q\left(z_i \mid z_{\mathrm{pa}(i)}\right)\]

TreeDiffusion

  • DDPM tutorial is available here
  • Equations remain the same for the forward process
  • For the reverse process, first, a path is sampled from the root to a leaf node \(\textit{l}\)

    A sequence of stochastic transformations is applied to the root embedding along this path

  • The hierarchical conditioning information is derived from \(\textbf{z}_{\mathcal{P}_l}\)
  • These embeddings are processed by a dedicated path encoder which aggregates the information to produce the conditioning signal \(\textbf{y}_l\) :
\[\mathbf{y}_l = \sum_{i \in \mathcal{P}_l} \left( f_{\text{embed}}(\mathbf{z}_i) + f_{\text{node}}(i) \right)\]
  • \(f_{embed}\) and \(f_{node}\) are implemented as projection blocks consisting of two MLP layers with a SiLU activation in-between (they are jointly trained with the diffusion model)
  • Link of the architecture here

For each node in the path, its embedding and corresponding node index are projected independently into the time embedding dimension of the U-Net decoder.

Currently, sampling is limited to paths originating from the root

  • The reverse process is like a DDPM using the \(\textbf{y}_l\) signal as the conditioning term
  • They used DDIM to accelerate inference

TreeVAE + Diffusion

  • Similar method than DiffuseVAE [1]
  • You take the output of a VAE-based model and you apply a diffusion model on it to get better reconstructed samples
  • You keep the representation of a VAE while improving the reconstruction part
  • TreeVAE + Diffusion is the same process than DiffuseVAE: You take the reconstructed image from the decoder of one leaf and you give it to a diffusion model to refine the reconstruction (in this case, there is no condition on any latent information from the hierarchical structure)

 

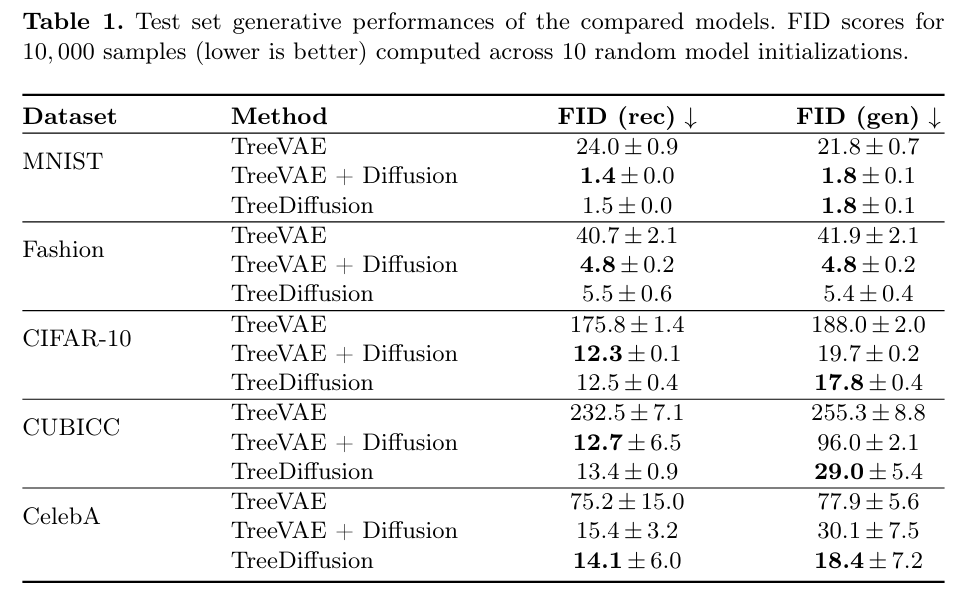
Results

  • The naive approach performs better at image reconstruction rather than generation

    TreeVAE + Diffusion model begins denoising from TreeVAE reconstructions, thereby making it highly dependent on the reconstruction quality provided by TreeVAE.

  • TreeDiffusion achieves a better balance between reconstruction and generation quality
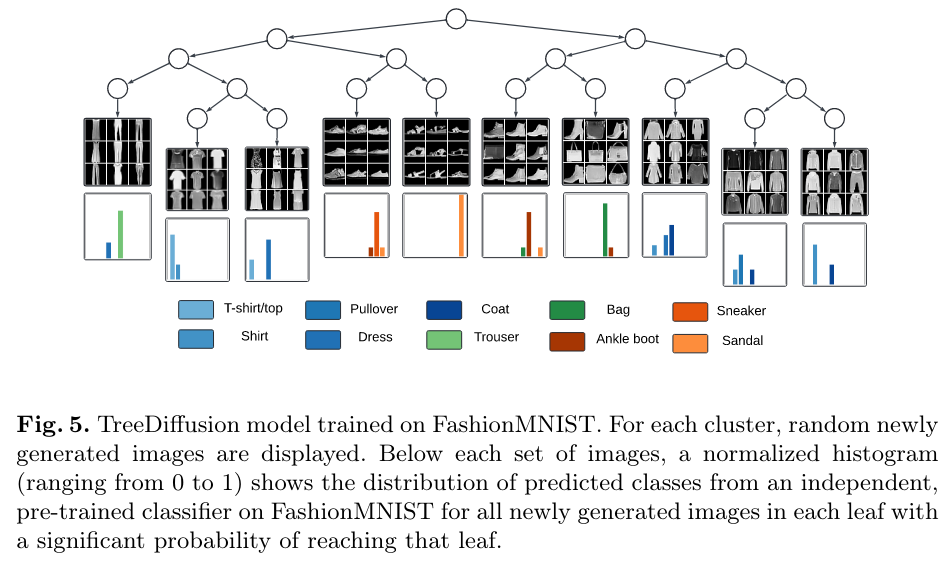
  • For each generation, they sample the root embedding, then select a path through the tree and refine the representations along this path until a leaf is reached
  • TreeDiffusion produces sharper images for all clusters but also generates a greater diversity of images
  • To quantitatively evaluate cluster retention in generated images, a classifier is trained on the original labeled dataset and then used to predict the classes of TreeDiffusion-generated samples
  • The “purity” of leaf nodes is assessed by examining whether generated samples are consistently classified into one or a small number of classes
  • High classification consistency indicates that TreeDiffusion effectively preserves hierarchical cluster information in its outputs
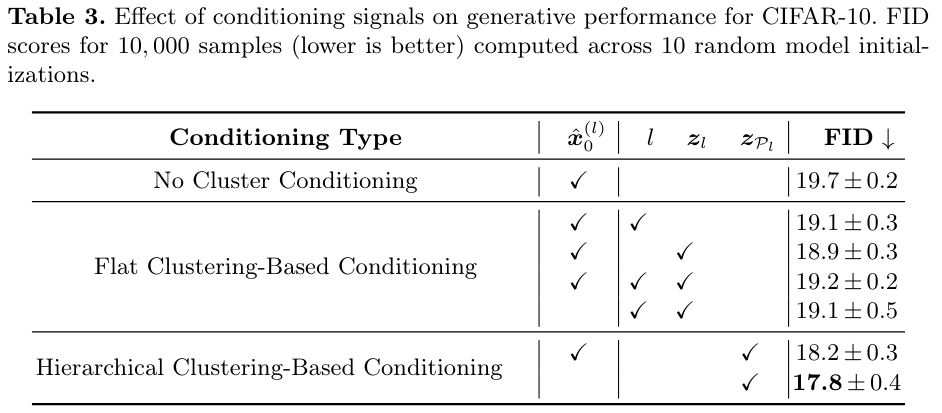
  • Conditioning on hierarchical representations improves cluster-specific generative quality
  • Ablation study on the conditional information \(\textbf{y}_l\)

    Note that the first row in the table represents the TreeVAE + Diffusion model from the previous experiments, whereas the last row corresponds to the proposed TreeDiffusion method

 

Conclusions

  • TreeVAE provides effective hierarchical clustering representations, while the diffusion model enables high-quality image generation.

[1] Pandey, Kushagra and Mukherjee, Avideep and Rai, Piyush and Kumar, Abhishek (preprint 2022). Diffusevae: Efficient, controllable and high-fidelity generation from low-dimensional latents.